Xét `Delta ABC ` ta có

`AM` là tia phân giác của `hat(BAC)`

`=> (BM)/(CM) = (AB)/(AC)`

`=> CM = (BM*AC)/(AB)`

Mà `AB =12cm,AC=15cm,BM=8cm`

`=> CM=(8*15)/12=10(cm)`

Do M là trung điểm của BC nên:

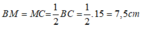
Theo tính chất tia phân giác của góc ta có:

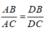
Suy ra:

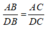
Theo tính chất của dãy tỉ số bằng nhau ta có:

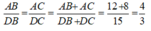
Suy ra:

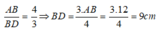
Do đó:

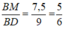
Chọn đáp án A 

Do M là trung điểm của BC nên:

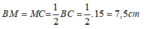
Theo tính chất tia phân giác của góc ta có:

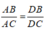
Suy ra:

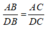
Theo tính chất của dãy tỉ số bằng nhau ta có:

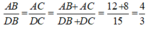
Suy ra:

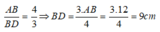
Do đó:

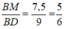
Chọn đáp án A

a Tam giác ABC cân tại A => AB=AC=15

Tia p/g BM

=> Theo tính chất đương p/g ta có

MC=AC-AM

=>

=> AM= 9

=> MC=AC-AM=15-9=6

BM vuông góc BN

=> BM là tia p/g góc ngoài tại B

=>

=> NC.BA=BC.NA

NC.BA-BC.NA=0

NC.BA-BC(AC+CN)= 0

=> NC.15-10(15+CN)=0

=> NC=30

hơi rối

a: Xét ΔABC có BM là phân giác

nên AM/AB=CM/BC

=>AM/15=CM/10

=>AM/3=CM/2=(AM+CM)/(3+2)=15/5=3

=>AM=9cm; CM=6cm

b: BM vuông góc BN

=>BN là phân giác góc ngoài tại B

=>NC/NA=BC/BA

=>NC/(NC+15)=10/15=2/3

=>3NC=2NC+30

=>NC=30cm

a: Xét ΔABM và ΔACN có

\(\widehat{ABM}=\widehat{ACN}\)

AB=AC

\(\widehat{A}\) chung

Do đó: ΔABM=ΔACN

Suy ra: AM=AN=9cm và AB=AC=15cm

Xét ΔABC có BM là phân giác

nên AM/MC=AB/BC

=>15/BC=9/6=3/2

=>BC=10cm

b: Xét ΔABC có AM/AC=AN/AB

nên MN//BC

c: Xét ΔABC có MN//BC

nên AM/AC=MN/BC

=>MN/10=9/15=3/5

=>MN=6(cm)

Chọn A

Chọn đáp án A

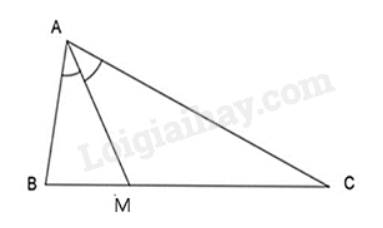
Vì \(AM\) là tia phân giác góc \(A\left( {M \in BC} \right)\) nên theo tính chất đường phân giác ta có:

\(\frac{{BM}}{{CM}} = \frac{{AB}}{{AC}};\frac{{BM}}{{AB}} = \frac{{CM}}{{AC}};\frac{{CM}}{{BM}} = \frac{{AC}}{{AB}};\frac{{AC}}{{CM}} = \frac{{AB}}{{BM}}\).

a/ Xét tg vuông BAC và tg vuông HAB có

\(\widehat{ACB}=\widehat{ABH}\) (cùng phụ với \(\widehat{BAC}\) )

b/

\(BC=\sqrt{AC^2-AB^2}\) (Pitago)

\(\Rightarrow BC=\sqrt{25^2-15^2}=20cm\)

\(\dfrac{MA}{AB}=\dfrac{MC}{BC}\) (T/c đường phân giác)

\(\Rightarrow\dfrac{MA}{15}=\dfrac{MC}{25}\Rightarrow\dfrac{MA}{MC}=\dfrac{15}{25}=\dfrac{3}{5}\)

\(\Rightarrow MC=\dfrac{AC}{3+5}x5=\dfrac{25}{8}x5=15,625cm\)

c/

\(AB^2=AH.AC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)

\(\Rightarrow AH=\dfrac{AB^2}{AC}\)

AM=AC-MC

HM=AM-AH

\(BH^2=AH.HC\)(trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích giữa 2 hình chiếu của 2 cạnh góc vuông trên cạnh huyền)

Xét tg vuông BHM

\(BM=\sqrt{BH^2+HM^2}\)

Ta có

\(AB\perp BC;MI\perp BC\) => MI//AB

\(\Rightarrow\dfrac{BI}{AM}=\dfrac{CI}{MC}\Rightarrow\dfrac{BI}{CI}=\dfrac{AM}{MC}\) (talet trong tg)

Từ đó tính được CI

Bạn tự thay số và tính toán

\(a.\) Xét \(\Delta BAC\) và \(\Delta HAB\) \(\left(\widehat{B}=\widehat{H}=90^o\right)\), ta có:
\(\widehat{A}\) là góc chung
\(\Rightarrow\Delta BAC\sim\Delta HAB\) \(\left(g-g\right)\)
\(b.\) Xét \(\Delta ABC\) vuông tại \(\widehat{B}\), ta có:
\(AC^2=AB^2+BC^2\) \(\left(Pytago\right)\)
\(\Rightarrow BC^2=AC^2-AB^2=25^2-15^2=625-225=400\)
\(\Rightarrow BC=\sqrt{400}=20\) \(\left(cm\right)\)
Do \(BM\) là đường phân giác của \(\Delta ABC\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{BC}{MC}\) \(\Rightarrow\dfrac{AB}{AC-MC}=\dfrac{BC}{MC}\)
\(\Rightarrow AB\cdot MC=BC\cdot\left(AC-MC\right)\)
\(\Leftrightarrow AB\cdot MC=AC\cdot BC-BC\cdot MC\)
\(\Leftrightarrow AB\cdot MC+BC\cdot MC=AC\cdot BC\)
\(\Leftrightarrow MC\left(AB+BC\right)=AC\cdot BC\)
\(\Leftrightarrow MC=\dfrac{AC\cdot BC}{AB+BC}=\dfrac{25\cdot20}{15+20}=\dfrac{500}{35}=\dfrac{100}{7}\approx14,29\) \(\left(cm\right)\)