a)+Có AB//Cx(gt)=> góc ABC= góc ECD(2 góc đồng vị )

Mà góc ABC =60 (vì tam giác ABC đều)=>góc ECD= ABC=60

+Có AC//Dy(gt)=> góc ACB= góc EDC (2 góc đồng vị)

 Mà góc ACB =60 (vì tam giác ABC đều)=>góc EDC= ACB=60

+Có ECD=60; EDC=60=>ECD=EDC=60

=>tam giác ECD đều (dhnb tam giác đều)

b) +Có góc ACB+ACD=180(kề bù)

    +Có góc ECD+ECB=180(kề bù)

     Mà góc ACB=ECD=60     

=>Góc ACD = góc ECB

Xét tam giác ACD và tam giác BCE

+Có CD=ED(tam giác ECD đều)

        góc ACD=góc ECB(cmt)

        AC=BC((tam giác ABC đều)

        =>tam giác ACD =BCE

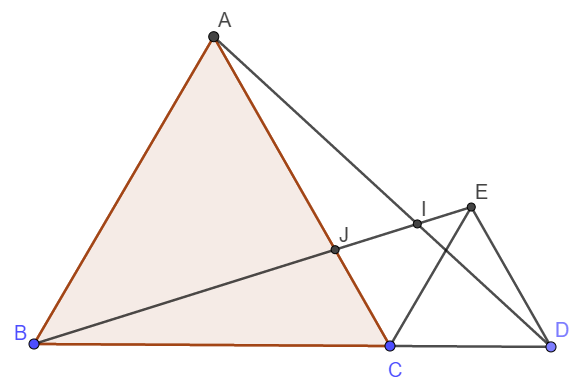
a) Do EC// AB nên \(\widehat{ECD}=\widehat{ABC}=60^o\)

Do ED// AC nên \(\widehat{EDC}=\widehat{ACB}=60^o\)

Xét tam giác ECD có \(\widehat{ECD}=\widehat{EDC}=60^o\Rightarrow\widehat{CED}=60^o\)

Suy ra ECD là tam giác đều.

b) Ta có :

\(\widehat{BCE}=\widehat{BCA}+\widehat{ACE}=60^o+\widehat{ACE}=\widehat{ECD}+\widehat{ACE}=\widehat{ACD}\)

Xét tam giác BCE và tam giác ACD có:

BC = AC (gt)

CD = CE (Do tam giác ECD đều)

\(\widehat{BCE}=\widehat{ACD}\)  (cmt)

\(\Rightarrow\Delta BCE=\Delta ACD\left(c-g-c\right)\)

\(\Rightarrow BE=AC\)

c) Do \(\Delta BCE=\Delta ACD\Rightarrow\widehat{CBI}=\widehat{CAI}\)

Vậy thì \(\widehat{CBJ}+\widehat{BJC}=\widehat{JAI}+\widehat{JAI}\)

\(\Rightarrow180^o-\left(\widehat{CBJ}+\widehat{BJC}\right)=180^o-\left(\widehat{JAI}+\widehat{JAI}\right)\)

\(\Rightarrow\widehat{AIJ}=\widehat{JCB}=60^o\)

\(\Rightarrow\widehat{BID}=180^o-60^o=120^o\)  (Hai góc kề bù)

\(\Rightarrow\widehat{BID}=2\widehat{BAC}\)

hình bạn tự vẽ nhé

xét tam giác BID và tam giác CIE có

    BI = IC

    góc DBI = góc ECI (so le trong)

   \(\widehat{DIB}=\widehat{EIC}\)ĐỐI ĐỈNH

 suy ra tam giác BID = tam giác CIE (g.c.g)

  suy ra BD = CE ( 2 cạnh tương ứng )

 b)  ta có \(\widehat{ABC}=\widehat{ACB},\widehat{ABC}=\widehat{xCB}\Rightarrow\widehat{ACB}=\widehat{xCB}\)

mà tia CB nằm giữa 2 tia CA và Cx nên CB là phân giác góc ACx

chúc bạn học giỏi

Ví  von hay lắm man

a) Vì AB // Cx nên góc ABC = BCE ( so le trong )

Xét ΔDBI và ΔECI có:

DB = EC (GT)

ABC = BCE ( chứng minh trên )

BI = CI (suy từ gt)

=> ΔDBI = ΔECI (c.g.c)

b) Do AB = AC nên ΔABC cân tại A

đc góc ABC = ACB (1)

mà AB // Cx => góc ABC = BCE (so le trong) (2)

Từ (1) và (2) suy ra ACB = BCE

Do đó CB là tia pg của góc ACE

c) Lại do ΔDBI = ΔECI nên góc BID = CIE (2 góc tương ứng)

mà 2 góc này đối nhau nên D, I, E thẳng hàng → đpcm

Chúc học tốt Tam Nguyen Thanh

thank you bạn nhìu nhé