
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nối B vs I. Xét tam giác BID vuông tại D, có:
BD2 = BI^2 - ID2 (1).Xét tam giác ICD vuông tại D, có:
DC2 = IC2 - ID2 (2).Từ (1) và (2) =>
=> BD2 - DC2
= BI2 - ID2 - IC2 + ID2
= BI2 - IC2
= BI2 - AI2 (vì AM=CM)
= AB2=> AB2 = BD2 - DC2 (đpcm)

\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)

Bài 1:
a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>BC=10(cm)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔHAB vuông tại H có HG là đường cao
nên \(AG\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HK là đường cao
nên \(AK\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AG\cdot AB=AK\cdot AC\)

b) Ta có:
\(\widehat{B}=180^o-90^o-42^o=48^o\)
Xét tam giác ABC vuông tại A ta có:
\(cosB=\dfrac{AB}{BM}\Rightarrow cos48^o=\dfrac{6}{BM}\)
\(\Rightarrow BM=\dfrac{6}{cos48^o}\approx9\left(cm\right)\)
Mà: \(sinB=\dfrac{AM}{BM}\Rightarrow sin48^o=\dfrac{AM}{9}\)
\(\Rightarrow AM=9\cdot sin48^o\approx6,7\left(cm\right)\)

Vì \(AC\perp AB;HD\perp AB\Rightarrow AC//HD\)
Áp dụng hệ quả Ta lét ta có : \(\frac{BD}{BC}=\frac{HD}{AC}\)(*)
Vì AD là đường phân giác ^A nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Lại có : \(BC^2=AB^2+AC^2=36+64=100\Rightarrow BC=10\)cm
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{10}{14}=\frac{5}{7}\)
\(\Rightarrow DC=\frac{5}{7}AC=\frac{5}{7}.8=\frac{40}{7}\)cm ; \(BD=\frac{5}{7}AB=\frac{5}{7}.6=\frac{30}{7}\)cm
Thay vào (*) ta được : \(\frac{\frac{30}{7}}{10}=\frac{HD}{8}\Rightarrow10HD=\frac{240}{7}\Rightarrow HD=\frac{24}{7}\)cm
Có : \(\frac{BH}{AB}=\frac{HD}{AC}\)( hệ quả Ta lét ) \(\Rightarrow BH=\frac{AB.HD}{AC}=\frac{6.\frac{24}{7}}{8}=\frac{18}{7}\)cm
\(\Rightarrow AH=AB-BH=6-\frac{18}{7}=\frac{24}{7}\)cm
Áp dụng định lí Pytago tam giác AHD vuông tại H ta có :
\(AD^2=AH^2+HD^2=\left(\frac{24}{7}\right)^2+\left(\frac{24}{7}\right)^2=2\left(\frac{24}{7}\right)^2\)
\(\Rightarrow AD=\frac{24\sqrt{2}}{7}\)cm o.O bạn check lại xem nhé

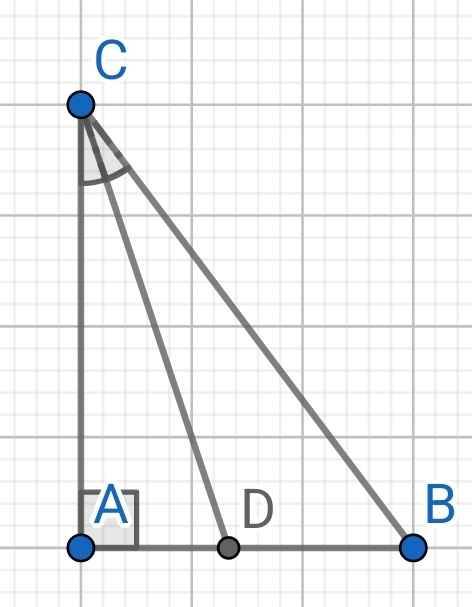 Do ∆ABC vuông tại A
Do ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC.1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AC² + AD² (Pytago)
= 8² + (8/3)²
= 640/9
⇒ CD = 8√10/3 (cm)

Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Áp dụng HTL:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
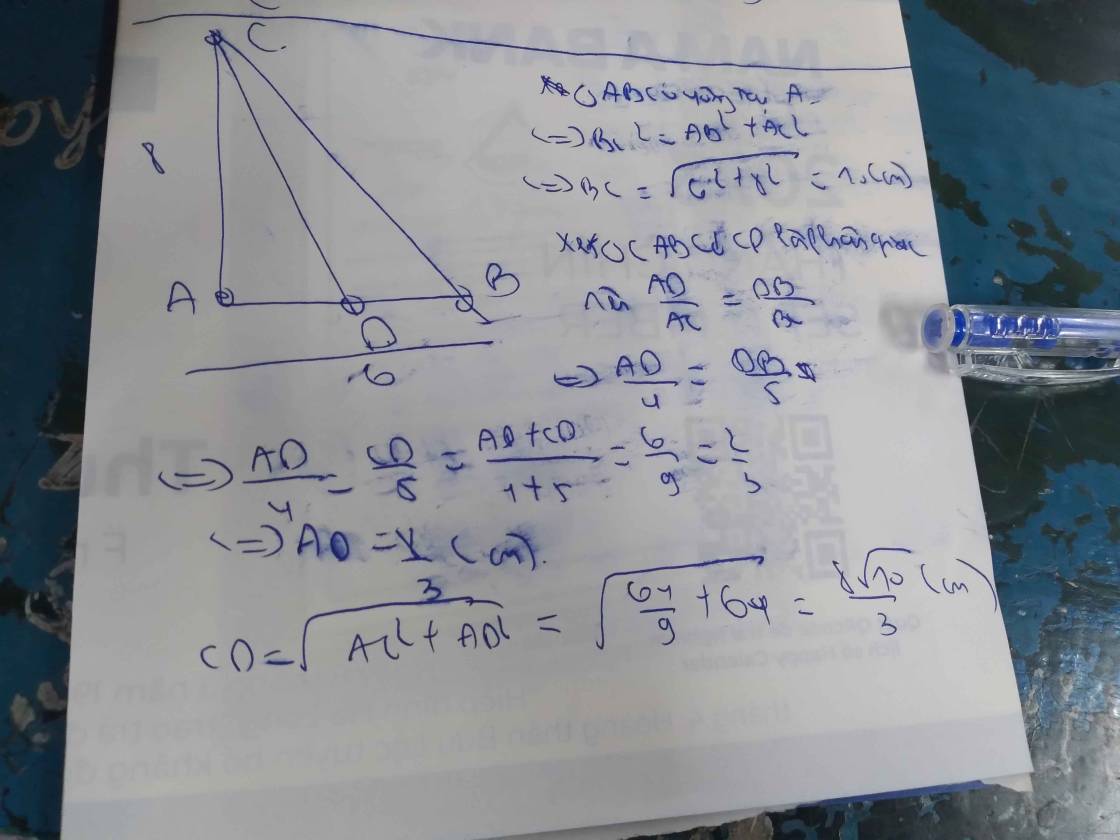
Xét tam giác ABC vuông tại A áp dụn Py-ta-go ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}\)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\)
\(\Rightarrow\widehat{B}\approx53^o\)
\(\Rightarrow\widehat{C}=90^o-53^o\approx37^o\)