Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có ∆AHD có AH = HD và AHD = 90 nên ∆AHD vuông cân tại H
=> HAD = HDA = 45
=> ADE = 90 - HDA = 45
Tứ giác ABDE nội tiếp đường tròn vì có ABE + BDE = 180
=> ABE = ADE = 45 (1)
Mà ∆ABE lại có ABE = 90 (2)
Từ (1) và (2) => ∆ABE vuông cân tại A
=> AB = AE
a/ Ta có AE // AH( vì cùng vuông góc BC)
=> HD/HC = AE/AC
=> AC.HD = AE.HC (1)
Ta lại có AB = AE (2)
AH = HD (3)
Từ (1), (2), (3) => AB.HC = AC.AH
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
Gọi AM cắt DE tại I
Theo tính chất hình chữ nhật ADHE : \(\widehat{E_1}=\widehat{HAC}=\widehat{MBA};\widehat{A_1}=\widehat{D_1}=\widehat{AHE}=\widehat{MCA}\)
\(\Rightarrow\widehat{A_1}=\widehat{ACM}\Rightarrow\Delta ACM\)cân tại M \(\Rightarrow MA=MC\)(*)
Do \(\Delta AID\)vuông tại I suy ra
\(\widehat{DAM}+\widehat{D_1}=90^0\Leftrightarrow\widehat{DAM}+\widehat{DAH}=90^0\left(1\right)\)
\(\widehat{ABM}+\widehat{DAH}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{DAM}=\widehat{ABM}\)
\(\Rightarrow\Delta ABM\)cân tại M \(\Rightarrow MA=MB\)(**)
Từ (*);(**) suy ra MB=MC hay M là trung điểm BC . Do MF//AC suy ra
\(\widehat{MFC}=\widehat{ACF}\)
Mà
\(\widehat{ACF}=\widehat{MCF}\Rightarrow\widehat{MFC}=\widehat{MCF}\Rightarrow\Delta MFC\)cân tại M suy ra MC=MF
Mà MB=MC suy ra 
\(\Delta BFC\) có FM là trung tuyến 
\(FM=\frac{1}{2}BC\Rightarrow\) \(\Delta BFC\)vuông tại F hay 
\(BF\perp CF\left(đpcm\right)\)
Xét \(\Delta ABK\),ta có: BE là phân giác \(\angle ABK,BE\bot AK\)
\(\Rightarrow\Delta ABK\) cân tại B \(\Rightarrow BE\) là trung trực AK
Xét \(\Delta ABD\) và \(\Delta KBD:\) Ta có: \(\left\{{}\begin{matrix}AB=BK\\BDchung\\\angle ABD=\angle KBD\end{matrix}\right.\)
\(\Rightarrow\Delta ABD\sim\Delta KBD\left(c-g-c\right)\Rightarrow\angle BKD=\angle BAD=90\)
Ta có: \(\angle BAD+\angle BKD=90+90=180\Rightarrow BAKD\) nội tiếp
\(\Rightarrow\angle AKD=\angle ABD=\angle KBD=\angle KAH\left(=90-\angle BKA\right)\)
\(\Rightarrow\)\(AI\parallel KD\)
Vì \(I\in BE\Rightarrow IA=IK\Rightarrow\Delta IAK\) cân tại I \(\Rightarrow\angle IKA=\angle IAK\)
BADK nội tiếp \(\Rightarrow\angle KAD=\angle KBD=\angle ABD=\angle AKD\)
\(\Rightarrow\angle IKA=\angle DAK\Rightarrow\)\(IK\parallel AD\Rightarrow AIKD\) là hình bình hành
mà \(IA=IK\Rightarrow IKDA\) là hình thoi
a) Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{16^2+12^2}=20\left(cm\right)\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.16}{20}=\dfrac{48}{5}\left(cm\right)\)
Ta có: \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{16^2}{20}=\dfrac{64}{5}\left(cm\right)\)
Ta có: \(sinB=\dfrac{AC}{BC}=\dfrac{12}{20}=\dfrac{3}{5}\Rightarrow\angle B\approx37\)
b) tam giác AHE vuông tại H có HN là đường cao \(\Rightarrow AN.AE=AH^2\)
tam giác ABC vuông tại A có AH là đường cao \(\Rightarrow AH^2=HB.HC\)
\(\Rightarrow AN.AE=HB.HC\)
c) tam giác AHB vuông tại H có HM là đường cao \(\Rightarrow AH^2=AM.AB\)
\(\Rightarrow AN.AE=AM.AB\Rightarrow\dfrac{AM}{AE}=\dfrac{AN}{AB}\)
Xét \(\Delta AMN\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle EABchung\\\dfrac{AM}{AE}=\dfrac{AN}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta AEB\left(c-g-c\right)\Rightarrow\dfrac{AE}{AM}=\dfrac{BE}{MN}\)
mà \(BE=3MN\Rightarrow\dfrac{BE}{MN}=3\Rightarrow\dfrac{AE}{AM}=3\Rightarrow AE=3AM\)
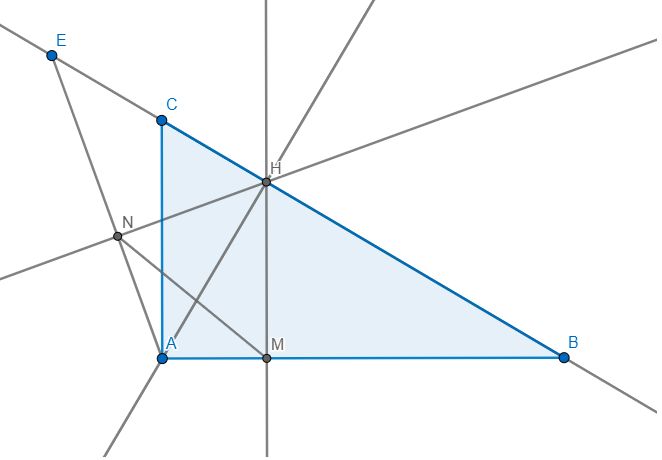
a/
Ta có
\(\widehat{A}=90^o;\widehat{MHN}=90^o\) => A và H cùng nhìn MN dưới 1 góc vuông nên A; H thuộc đường tròn đường kính MN => A; M; H; N cùng thuộc 1 đường tròn
Xét tg vuông AHC có
\(MA=MC\Rightarrow HM=MA=MC=\dfrac{AC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AMH cân tại M \(\Rightarrow\widehat{MAH}=\widehat{MHA}\)
Mà
\(\widehat{NAH}+\widehat{MAH}=\widehat{A}=90^o\)
\(\widehat{NHA}+\widehat{MHA}=\widehat{MHN}=90^o\)
\(\Rightarrow\widehat{NAH}=\widehat{NHA}\) => tg NAH cân tại N => NA=HN (1)
Xét tg vuông ABH có
\(\widehat{NAH}+\widehat{B}=90^o\)
\(\widehat{NHA}+\widehat{NHB}=\widehat{AHB}=90^o\)
Mà \(\widehat{NAH}=\widehat{NHA}\) (cmt)
\(\Rightarrow\widehat{B}=\widehat{NHB}\) => tg BHN cân tại N => NB=HN (2)
Từ (1) và (2) => NA=NB => N là trung điểm AB
b/
Ta có
NA=NB (cmt); MA=MC (gt) => MN là đường trung bình của tg ABC
=> MN//BC
Gọi O là giao của MN với AH. Xét tg ABH có
MN//BC => NO//BH
NA=NB (cmt)
=> OA=OH (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại) => O à trung điểm AH
Ta có
\(HE\perp AB\left(gt\right);AC\perp AB\left(gt\right)\) => HE//AC => HE//AF
\(HF\perp AC\left(gt\right);AB\perp AC\left(gt\right)\) => HF//AB => HF//AN
=> AEHF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Gọi O' là giao của EF với AH => O'A=O'H (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O' là trung điểm của AH
Mà O cũng là trung điểm của AH (cmt)
=> \(O'\equiv O\) => AH; MN; EF cùng đi qua O
Xét \(\Delta ABE\) có
\(AE=AB\Rightarrow\Delta ABE\) cân tại A
Ta có \(MB=ME\left(gt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{EAM}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^o}{2}=45^o\) và \(AM\perp BE\)(Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao và đường phân giác của góc ở đỉnh tg cân)
Ta có M và H cùng nhìn AB dưới một góc \(90^o\) => ABHM là tứ giác nội tiếp
\(\Rightarrow\widehat{ABE}=\widehat{AHM}=45^o\) (góc nt cùng chắn cung AM)
\(\Rightarrow\widehat{CHM}=\widehat{AHC}-\widehat{AHM}=90^o-45^o=45^o\)
\(\Rightarrow\widehat{AHM}=\widehat{CHM}=45^o\) => HM là phân giác của \(\widehat{AHC}\)