Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác BADC có
M là trung điểm của AC
M là trung điểm của BD
Do đó: BADC là hình bình hành
mà \(\widehat{ABC}=90^0\)
nên BADC là hình chữ nhật

a: M đối xứng A qua BC
nên BC là trung trực của AM
=>BA=BM; CA=CM
mà BA=CA
nên BA=BM=CA=CM
=>ABMC là hình thoi
b: Xét tứ giác AHCI có
K là trung điểm chung của AC và HI
góc AHC=90 độ
Do đó: AHCI là hình chữ nhật
c: Xét ΔBAC có CH/CB=CK/CA
nen HK//AB và HK=AB/2
=>HK//AD và HK=AD
=>ADHK là hình bình hành
=>AH cắt DK tại trung điểm của mỗi đường(1)
Xét tứ giác AIHB có
AI//HB
AI=HB
Do đó: AIHB là hình bình hành
=>AH cắt IB tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AH,IB,DK đồng quy

a: Xét tứ giác AKIH có
\(\widehat{AKI}=\widehat{AHI}=\widehat{HAK}=90^0\)
Do đó: AKIH là hình chữ nhật

Bn tự vẽ hình nha
a, Xét tứ giác ABCD có
MA=MC=1/2AC( m là trung điểm AC-gt)
MB=MD=1/2BD(B đối D qua M-gt)
Mà BD cắt AC tại M
-> ABCD là hình bình hành

a) Do B và D đối xứng qua M
\(\Rightarrow\) M là trung điểm BD
Tứ giác ABCD có:
M là trung điểm AC (gt)
M là trung điểm BD (cmt)
\(\Rightarrow\) ABCD là hình bình hành (tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
b) Do ABCD là hình bình hành
\(\Rightarrow\) AB // CD và AB = CD
\(\Rightarrow\) AN // CD
Do B và N đối xứng nhau qua A
\(\Rightarrow AN=AB\)
Mà AB = CD (cmt)
\(\Rightarrow\) AN = CD
Do AB \(\perp\) AC (\(\Delta ABC\) vuông tại A)
\(\Rightarrow AN\perp AC\)
\(\Rightarrow\widehat{CAN}=90^0\)
Tứ giác ACDN có:
AN // CD (cmt)
AN = CD (cmt)
\(\Rightarrow ACDN\) là hình bình hành
Mà \(\widehat{CAN}=90^0\)
\(\Rightarrow ACDN\) là hình chữ nhật (hình bình hành có một góc vuông)
c) Gọi E là giao điểm của MN và BC
Do AK // MN (gt)
\(\Rightarrow AK\) // ME và AK // NE
\(\Delta BNE\) có
AK // NE
A là trung điểm BN
\(\Rightarrow\) K là trung điểm BE
\(\Rightarrow KB=KE\)
\(\Delta AKC\) có:
AK // ME (cmt)
M là trung điểm AC
\(\Rightarrow\) E là trung điểm CK
\(\Rightarrow\) KC = 2 KE
Mà KB = KE (cmt)
\(\Rightarrow\) KC = 2 KB

b: Xét tứ giác AHCK có
E là trung điểm của AC
E là trung điểm của HK
Do đó: AHCK là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCK là hình chữ nhật

a)
Ta có: MB = MC; MA = MD (gt)
⇒ Tứ giác ABDC là hình bình hành
Mà: ∠A = 90°
⇒ Tứ giác ABDC là hình chữ nhật (đpcm)
b)
Gọi O là giao điểm của AC và AE
ΔAED có: OA = OE (E đối xứng với A qua BC); MA = MD (gt)
⇒ OM là đường trung bình của ΔAED
⇒ OM // ED (1)
Vì: E đối xứng với A qua BC
⇒ BC là đường trung trực của AE
⇒ BC ⊥ AE hay OM ⊥ AE (2)
Từ (1), (2) ⇒ ED ⊥ AE (đpcm)
c)
Ta có: BC // ED (OM // ED)
⇒ Tứ giác BEDC là hình thang
Ta có: BD = AC (Tứ giác ABDC là hình chữ nhật) (a)
ΔAEC có: CO vừa là đường trung tuyến vừa là đường cao
⇒ ΔAEC cân tại C ⇒ CA = CE (b)
Từ (a), (b) ⇒ BD = EC
Hình thang BEDC có: BD = EC
⇒ Tứ giác BEDC là hình thang cân

b: Xét tứ giác ANBE có
M là trung điểm của AB
M là trung điểm của NE
Do đó: ANBE là hình bình hành
mà NA=NB
nên ANBE là hình thoi

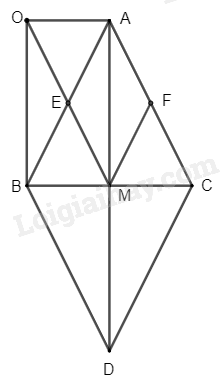
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi