TV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
7 – 1 < CA < 7 + 1
6 < CA < 8
Mà CA là số nguyên
CA = 7 cm.
Vậy CA = 7 cm.
b) Áp dụng bất đẳng thức tam giác trong tam giác ABC, ta có:
AB + CA > BC
2 + CA > 6
CA > 4 cm
Mà CA là số nguyên và CA < 6 ( vì BC = 6 cm là cạnh lớn nhất của tam giác)
CA = 5 cm
Vậy CA = 5 cm.
HL
27 tháng 7 2015
Goi a;b;c lan luot la AB;AC;BC
Ta co:\(AB:BC:AC=2:3:5\Rightarrow\frac{AB}{2}=\frac{BC}{3}=\frac{AC}{5}\)
Ap dung tinh chat day ti so bang nhau\(\frac{AB}{2}=\frac{BC}{3}=\frac{AC}{5}=\frac{AB+BC+AC}{2+3+5}=\frac{50}{10}=5\)
\(\Rightarrow\frac{AB}{2}=5\Rightarrow AB=10\)
\(\Rightarrow\frac{BC}{3}=5\Rightarrow BC=15\)
\(\Rightarrow\frac{AC}{5}=5\Rightarrow AC=25\)
17 tháng 9 2023
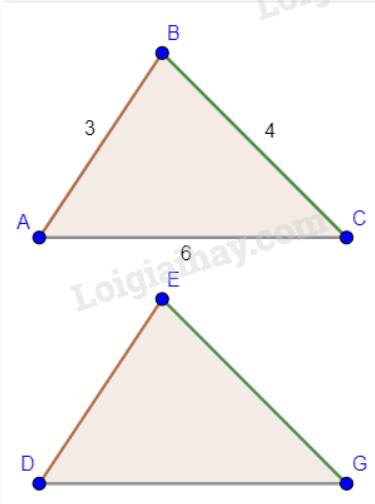
\(\Delta ABC = \Delta DEG\) nên AB = DE, BC = EG, CA = GD.
Vậy độ dài các cạnh của tam giác DEG lần lượt là: \(DE = 3\)cm,\(EG = 4\)cm,\(GD = 6\)cm.
17 tháng 9 2023
a) Trong tam giác ABC: \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 42^\circ - 37^\circ = 101^\circ \).
b) Trong tam giác ABC: \(\widehat B < \widehat A < \widehat C\)nên \(AC < BC < AB\). (Vì AC đối diện với góc B; BC đối diện với góc A; AB đối diện với góc C).