Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=[-2;4)
B=(0;5]
=>\(A\cap B=\left(0;4\right)\)
\(A\cup B=\left[-2;5\right]\)
A\B=[-2;0]
B\A=[4;5]

Để A giao B bằng rỗng thì 3a+1<0 và 2a>5
=>a<-1/3 hoặc a>5/2
=>Để A giao B khác rỗng thì a>=-1/3 và a<=5/2
=>-1/3<=a<=5/2

Điều kiện để A xác định là:
\(m-1< 8\)
\(\Leftrightarrow m< 8+1\Leftrightarrow m< 9\)
Để: \(A\backslash B=\varnothing\)
\(\Leftrightarrow A\subset B\) \(\Rightarrow2\le m-1\)
\(\Leftrightarrow m\ge3\)
kết hợp với điều kiện:
\(\Rightarrow3\le m< 9\)

Để tập hợp A và B có nghĩa thì:
\(m-4\le1\Leftrightarrow m\le5\) (1)
\(m>-3\) (2)
Từ (1) và (2) \(\Rightarrow-3< m\le5\)
Mà: \(A\cup B=B\)
\(\Rightarrow A\subset B\)
\(\Rightarrow\left\{{}\begin{matrix}m-4>-3\\m\ge1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>-3+4\\m\ge1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ge1\end{matrix}\right.\Leftrightarrow m>1\)
Mà: \(-3< m\le5\)
\(\Rightarrow1< m\le5\)
\(\Rightarrow m=\left\{2;3;4;5\right\}\)
Tổng là: có 4 giá trị m nguyên thỏa mãn

Lời giải:
Để $A\cap B$ rỗng thì:
$m\leq 2$ hoặc $m-9\geq 17$
$\Leftrightarrow m\leq 2$ hoặc $m\geq 26$

\(A=\left[m;m+1\right]\)
\(B=\left[0;3\right]\)
\(A\cap B=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1< 0\\m>3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\) thỏa mãn đề bài
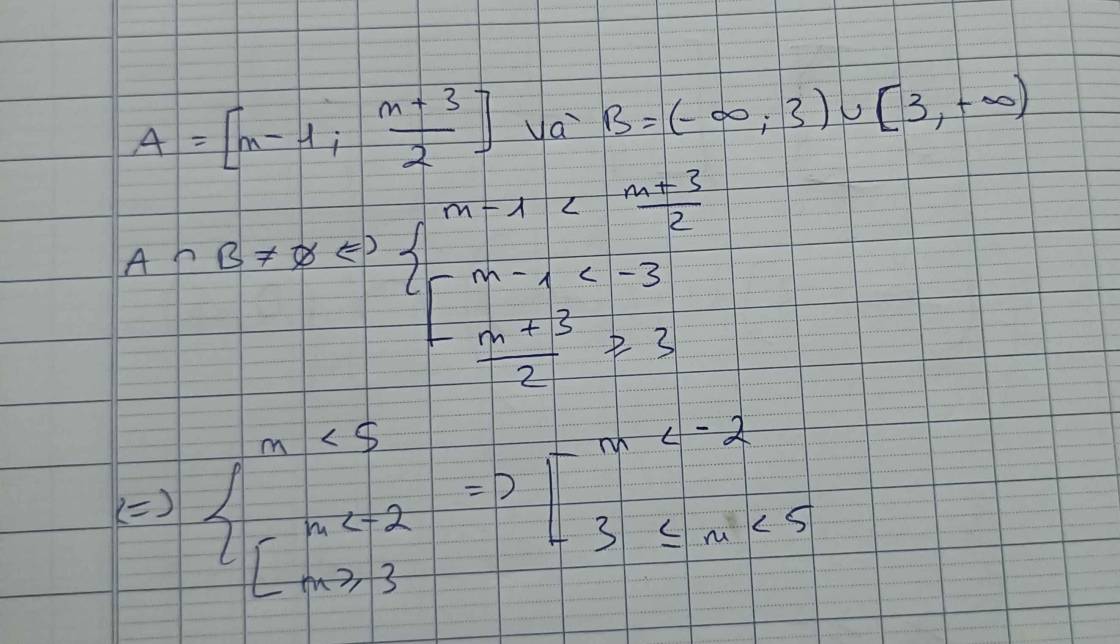
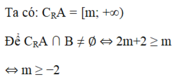
\(A\cap B=\varnothing\Leftrightarrow\left[{}\begin{matrix}m+2\le0\\m\ge5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m\le-2\\m\ge5\end{matrix}\right.\)
\(\Rightarrow A\cap B\ne\varnothing\Leftrightarrow-2< m< 5\)
Có \(4-\left(-1\right)+1=6\) số nguyên m
em thưa thầy em ko hiểu vì sao từ -2<m<5 lại có 4-(-1)+1=6 ạ