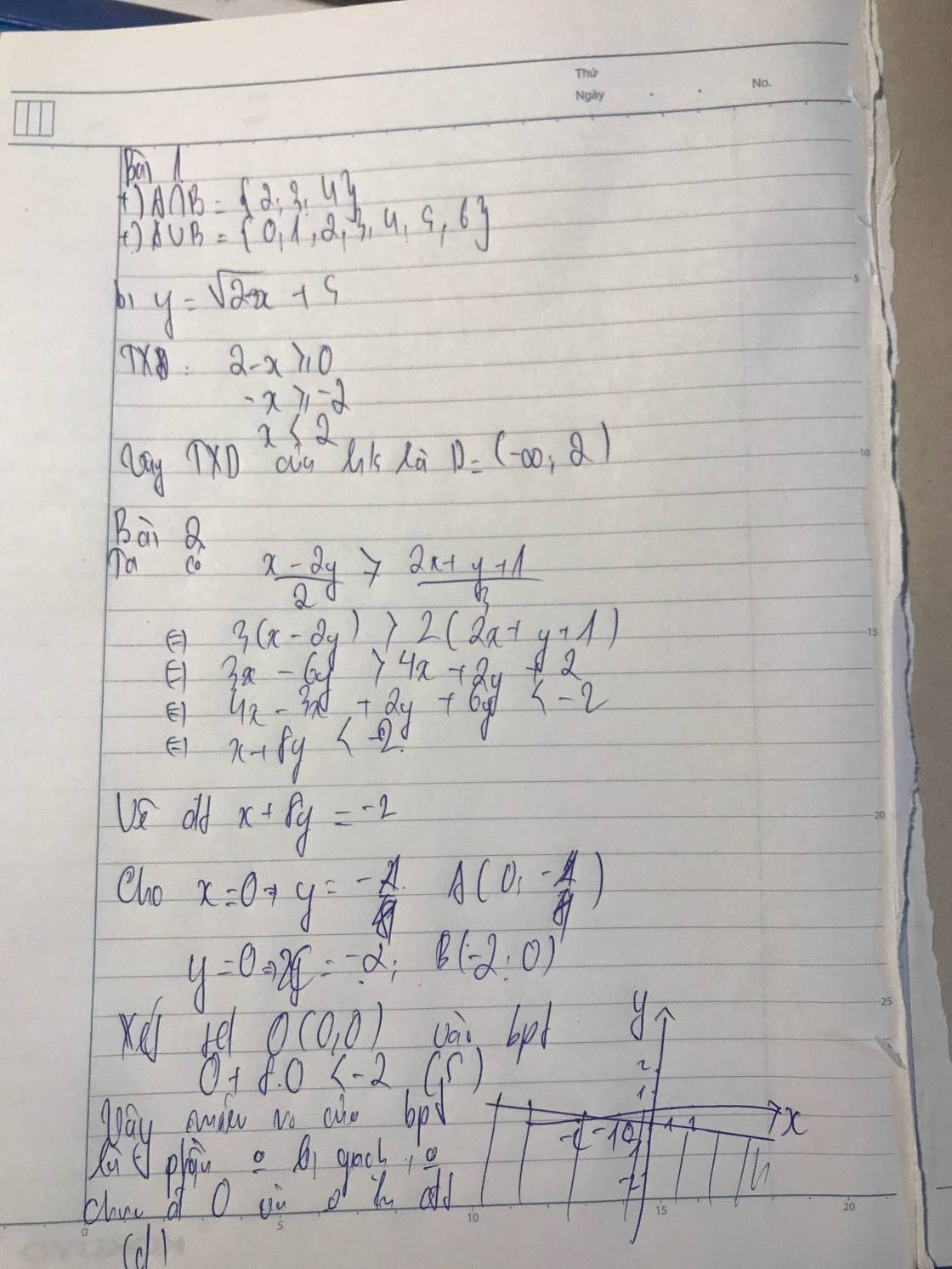\(A=\left(-3;-1\right)\cup\left(1;2\right)\)

\(B=\left(-1;+\infty\right)\)

\(C=\left(-\infty;2m\right)\)

\(A\cap B=\left(-3;-1\right)\)

Để \(A\cap B\cap C\ne\varnothing\Leftrightarrow2m\ge-1\)

\(\Leftrightarrow m\ge-\dfrac{1}{2}\)

Vậy \(m\ge-\dfrac{1}{2}\) thỏa đề bài

a: A=(-7/4; -1/2]

\(B=\left(-\dfrac{9}{2};-4\right)\cup\left(4;\dfrac{9}{2}\right)\)

\(C=\left(\dfrac{2}{3};+\infty\right)\)

b: \(\left(A\cap B\right)\cap C=\varnothing\)

\(\left(A\cup C\right)\cap\left(B\A\right)\)

\(=(-\dfrac{7}{4};-\dfrac{1}{2}]\cup\left(\dfrac{2}{3};+\infty\right)\cap\left[\left(-\dfrac{9}{2};-4\right)\cup\left(4;\dfrac{9}{2}\right)\right]\)

\(=\left(4;\dfrac{9}{2}\right)\)

a) \(A\cap B=\left\{2;3;4\right\}\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\)

b) Để hàm số xđ thì : \(2-x\ge0< =>-x\ge-2< =>x\le2\)

Ké ạ

Lời giải:

$A\cap B\cap C=A\cap (B\cap C)$

Để tập hợp trên khác rỗng thì trước hết $B\cap C\neq \varnothing$

Điều này xảy ra khi $2m>m\Leftrightarrow m>0$

Khi đó: $B\cap C=(m; 2m)$

$\Rightarrow A\cap B\cap C=((-3;-1)\cup (1;2))\cap (m; 2m)$

$=((-3;-1)\cap (m;2m))\cup ((1;2)\cap (m; 2m))$

$=(1;2)\cap (m; 2m)$ (do $m>0$)

Để $(1;2)\cap (m; 2m)\neq \varnothing$ thì:

\(\left\{\begin{matrix} 2m>1\\ m< 2\end{matrix}\right.\Leftrightarrow m\in (\frac{1}{2};2)\)

Vậy...........

\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\) 

\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)

\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)

\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)

\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)

\(\Leftrightarrow VT\le2g\left(x\right)\)

Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)

\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)

Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)

Ta có:

\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)

\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)

Vậy tập nghiệm của pt đã cho có đúng 1 phần tử

a) A ∪ B = (-∞; 15)

A ∩ B = [-2; 3)

b) Để A ⊂ B thì:

m - 1 > -2 và m + 4 ≤ 3

*) m - 1 > -2

m > -2 + 1

m > -1

*) m + 4 ≤ 3

m ≤ 3 - 4

m ≤ -1

Vậy không tìm được m thỏa mãn đề bài

a) A ∪ B = (-∞;15]

A∩B = [-2;3)