

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Chọn đáp án D
Ta có
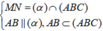
![]()
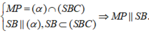
![]()
Khi đó ![]()
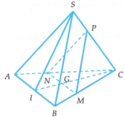
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
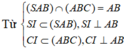
![]()
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0

Đáp án A
Giả sử tứ diện ABCD có AB;AC'AD đội một vuông góc ⇒ V A B C D = A B . A C . A D 6
Khi đó tứ diện MNPQ có MN;MP;MQ đội một vuông góc ⇒ V M . N P Q = M N . M P . M Q 6
Ta chứng minh được M N A B + M P A C + M Q A D = 1 ( dựa vào định lý Thalet), khi đó
M N . M P . M Q = A B . A C . A D . M N A B . M P A C . M Q A D ≤ A B . A C . A D . M N A B + M P A C + M Q A D 3 27 = A B . A C . A D 27
Vậy V M . N P Q = M N . M P . M Q 6 ≤ 1 27 . A B . A C . A D 6 = V 27 → V max = V 27

Đáp án B
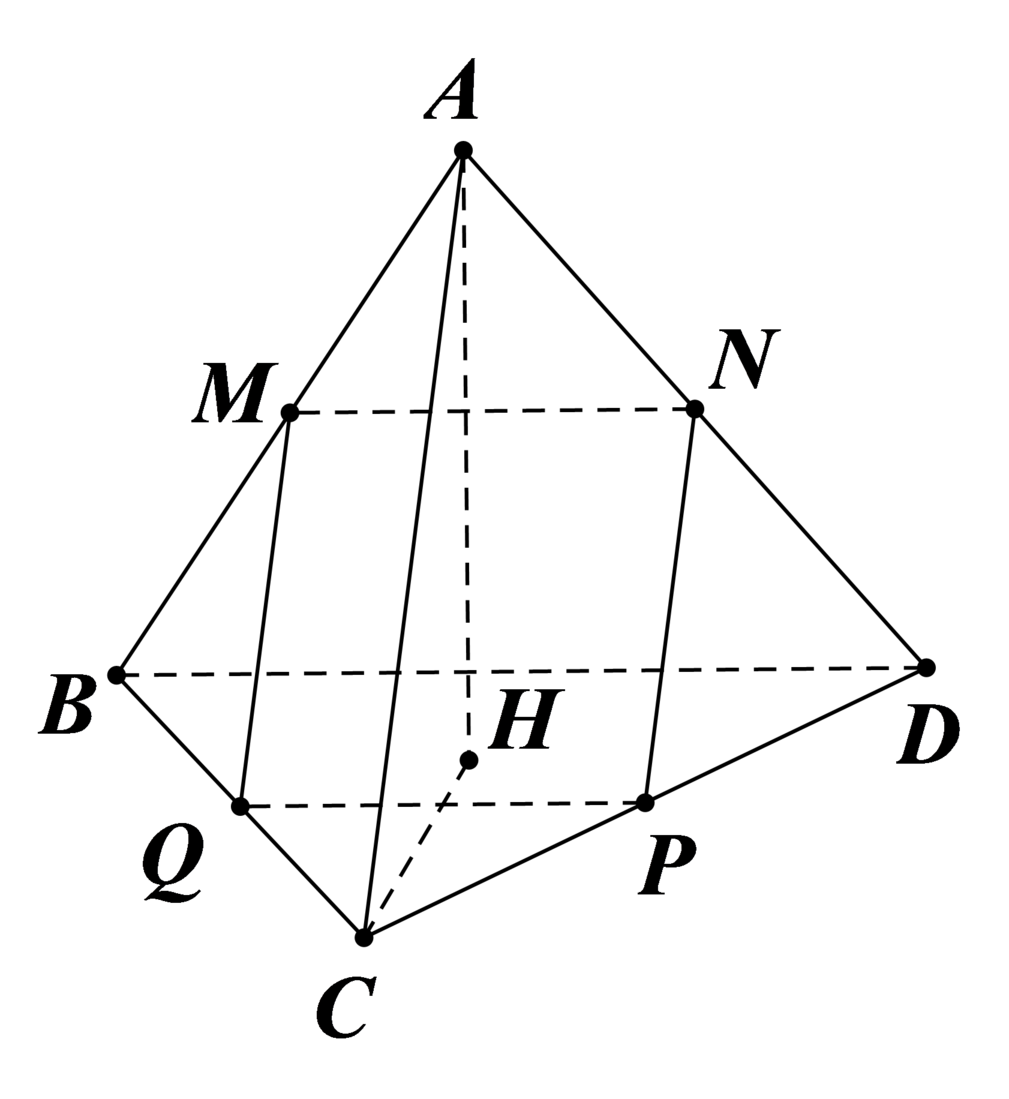
Gọi N, P, Q lần lượt là trung điểm của Ad, CD, BC.
Ta có: B D ⊥ A H C nên B D ⊥ A C . Do đó M N ⊥ N P . Mà MNPQ là hình bình hành.
Thiết diện là hình vuông MNPQ.