(Ghi chú: Muốn chứng minh hai số là nghịch đảo của nhau, ta chứng minh tích của hai số bằng 1.)

\(2^{2019}\) luôn là lũy thừa của số chẵn nên luôn chẵn, đặt \(2^{2019}=2k\)

\(\Rightarrow a=2^{2k}+5=4^k+5\)

\(4\equiv1\left(mod3\right)\Rightarrow4^k\equiv1\left(mod3\right)\)

\(\Rightarrow4^k+5\equiv0\left(mod3\right)\)

Hay \(a⋮3\), mà \(a>3\) nên a là hợp số

Dạ thầy ơi, dạ thầy chỉ cho em cái phần mod này được không ạ? Dạ em chưa hiểu lắm ạ

ta có 

\(A=111..1000..0+222..2+3=10^{2007}\left(1+10+..+10^{2004}\right)+2.\left(1+10+..+10^{2006}\right)+3\)

\(=10^{2007}.\frac{10^{2005}-1}{9}+2.\frac{10^{2007}-1}{9}+3=\frac{10^{2.2006}-10.10^{2006}+25}{9}=\left(\frac{10^{2006}-5}{3}\right)^2\)

rõ ràng Alà số tự nhiên nên \(\left(\frac{10^{2006}-5}{3}\right)\) là số tự nhiên, vậy ta có đpcm

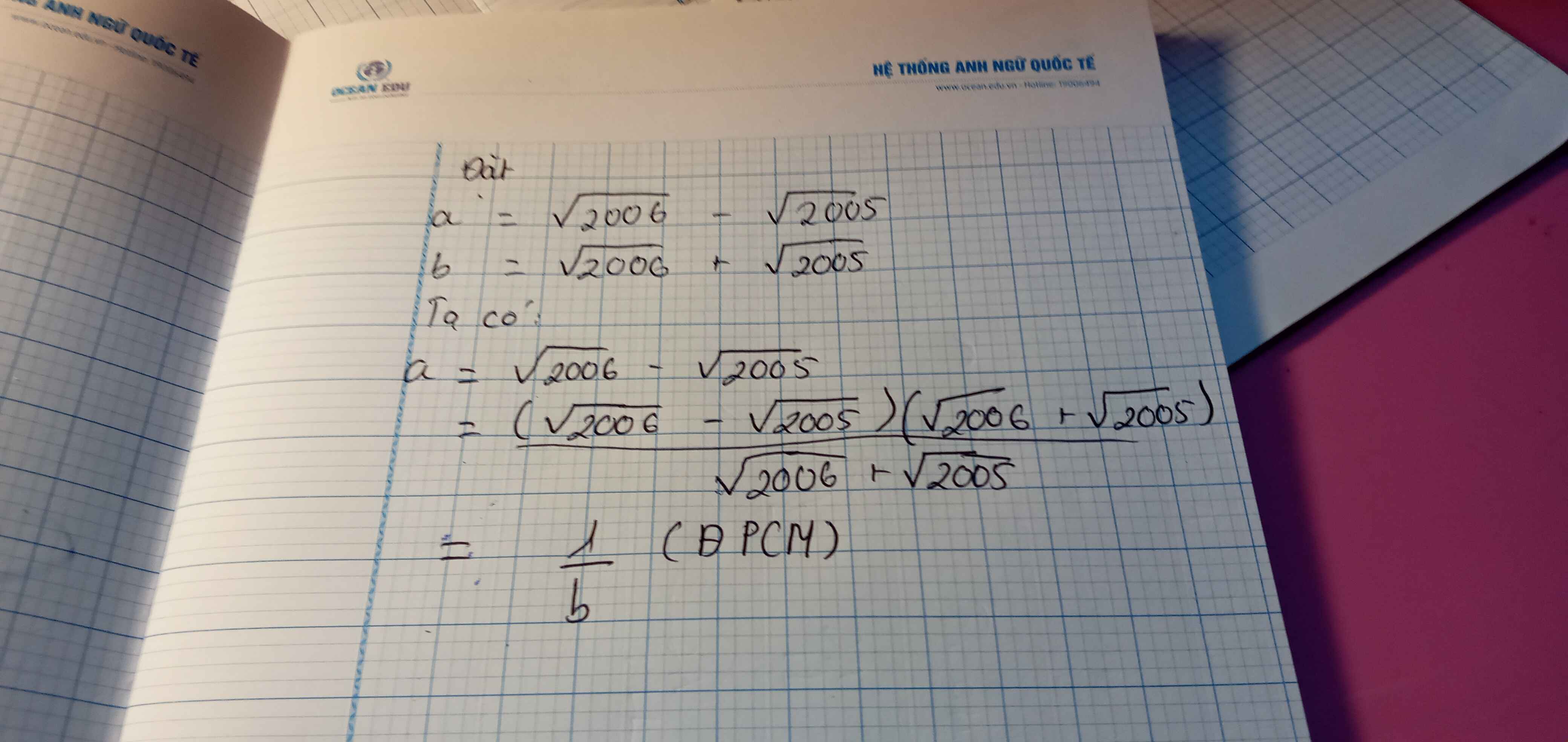
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)

Ta có 

\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)

\(\RightarrowĐfcm\)

Hằng đẳng thức a² - b² = (a - b).(a + b) <=> (a - b).(a + b) = a² - b²

bạn nên hỏi luôn khi cô giảng chứ, đừng giấu dốt nhé

Ta có :

A = 3k + 2

B = 6q + 2 hoặc 6q + 5

 6q + 2 có 6q chia hết cho 3 => 6q + 2 chia 3 dư 2

 6q + 5 = 6q + 3 + 2 có 6q + 3 chia hết cho 3 => 6q + 3 + 2 chia 3 dư 2

Vậy A = B

Hai bài này áp dụng hằng đẳng thức \(a^2-b^2=\left(a-b\right)\left(a+b\right)\) bạn nhé

a)

\(\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)\)

\(=2^2-\sqrt{3}^2\)

\(=4-3\)

\(=1\)

b)

Hai số nghịch đảo nhau là 2 số có tích của chúng bằng 1

Ví dụ

\(\frac{a}{b}\) và \(\frac{b}{a}\) ( hai số nghịch đảo )

\(\frac{a}{b}.\frac{b}{a}=1\)

Ta có

\(\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)\)

\(=\sqrt{2006}^2-\sqrt{2005}^2\)

\(=2006-2005\)

\(=1\)

=> Đpcm 

mơn pn nhìu