thx ban

Để \(\frac{2a+2b}{ab+1}\) là bình phương của 1 số nguyên thì 2a + 2b chia hết cho ab + 1; mà ab + 1 chia hết cho 2a + 2b => ab + 1 = 2b + 2a
=> \(\frac{2a+2b}{ab+1}\)=1 = 1²

Gọi ƯCLN(6n+5; 2n+1) là d. Ta có:

6n+5 chia hết cho d

2n+1 chia hết cho d => 6n+3 chia hết cho d

=> 6n+5-(6n+3) chia hết cho d

=> 2 chia hết cho d

=> d thuộc Ư(2)

Mà 2n+1 lẻ

=> không chia hết cho 2

=> d = 1

=> ƯCLN(6n+5; 2n+1) là d

=> 6n+5 và 2n+1 nguyên tố cùng nhau (đpcm)

6n + 5 chia hết cho n

2n + 1 chia hết cho a => 6n + 3 chia hết cho n

Mà 6n chia hết cho n 

=> UCLN(6n + 5 ; 6n + 3) = 1

Vậy là số nguyên tố cùng nhau

Cho hình vẽ, biết :

a) T a  có:   A ^ 1 = A ^ 2 = 70 0 (đối đỉnh). 

Do đó  A ^ 1 + B ^ = 70 0 + 110 0 = 180 0  

Suy ra Ax//By (vì có cặp góc trong cùng phía bù nhau). 

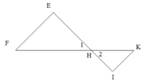
b) Ta có: F ^ = H ^ 1 ;   K ^ = H ^ 2  mµ  H ^ 1 = H ^ 2 ( đối đỉnh)

 nên F ^ = K ^ . Suy ra  EF//IK( vì có cặp góc so le trong bằng nhau).

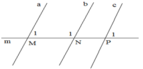
Ta có : M ^ 1 = P ^ 1 = 75 0 .

Suy ra a//c( vì có cặp góc đồng vị bằng nhau)

Ta có:

b N P ^  kÒ bï víi gãc N 1 , d o  ®ã: b N P ^ = 180 0 − 105 0 = 75 0 VËy  b N P ^ = P 1 ^ = 70 0

Suy ra b//c (vì có cặp góc đồng vị bằng nhau)

Giả sử trong 100 số nguyên dương đã cho không tồn tại 2 số nào bằng nhau

Không mất tính tổng quát, giả sử \(a_1< a_2< a_3< ...< a_{100}\)

\(\Rightarrow a_1\ge1;a_2\ge2;a_3\ge3;....;a_{100}\ge100\Rightarrow\frac{1}{a_1^2}+\frac{1}{a_2^2}+\frac{1}{a^2_3}...+\frac{1}{a^2_{100}}\le\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}\left(1\right)\)

Lại có: \(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}< 1+\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{99.100}=1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{99}-\frac{1}{100}=\frac{199}{100}\left(2\right)\)

Từ (1) và (2) => \(\frac{1}{a_1^2}+\frac{1}{a^2_2}+...+\frac{1}{a^2_{100}}< \frac{199}{100}\) trái với giả thiết

Vậy tồn tại ít nhất 2 số bằng nhau trong 100 số a₁,a₂,...,a₁₀₀