học thầy thanh ko làm mà đòi có ăn :))

đứa nào đấy :))))

Lớp 4 :))

lớp 4

a: Xét ΔOMN và ΔOPQ có

góc OMN=góc OPQ

góc MON=góc POQ

=>ΔOMN đồng dạng với ΔOPQ

=>OM/OP=ON/OQ=MN/PQ

=>OM*OQ=OP*ON

b: Xét ΔOMA vuông tại A và ΔOPB vuông tại B có

góc OMA=góc OPB

=>ΔOMA đồng dạng với ΔOPB

=>OM/OP=OA/OB=MN/PQ

Bài 10

a; Giao của d1 với trục ox là điểm có hoành độ thỏa mãn

     \(x\) - 3 = 0 ⇒ \(x\) = 3

Giao của d1 với trục oy là điểm có tung độ thỏa mãn y = 0 - 3 = -3

Giao của d2 với trục ox là điểm có hoành độ thỏa mãn 

     3 - \(x\) = 0 ⇒ \(x\) = 3

Giao của d2 với trục oy là điểm có tung độ thỏa mãn y = 3 - 0 = 3

Ta có đồ thị d1 và d2 như hình dưới 

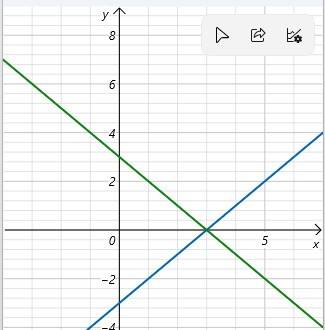
b; Giao của d1 và d2 là điểm có phương trình hoành độ thỏa mãn

\(x\) - 3 = 3 - \(x\)

2\(x\) = 6 

\(x\) = 6 : 2

\(x\) = 3; ⇒ y = 3- 3  =0 

Vậy giao của d1 và d2 là A(3;0)

Bài 9:

Giao của d1 với trục ox là điểm có hoành độ thỏa mãn 

              2\(x\) - 3  = 0 ⇒ \(x\) = \(\dfrac{3}{2}\)

Giao của d1 với trục oy là điểm có tung độ thỏa mãn

            y = 2.0 - 3  = - 3

Giao của d2 với trục ox là điểm có hoành độ thỏa mãn 

         -3 - \(x\) = 0 ⇒ \(x\) = 0

  Giao của d2 với trục oy là điểm có tung độ thỏa mãn

        y = -3 - 0 = -3

Ta có đồ thị như hình dưới đây

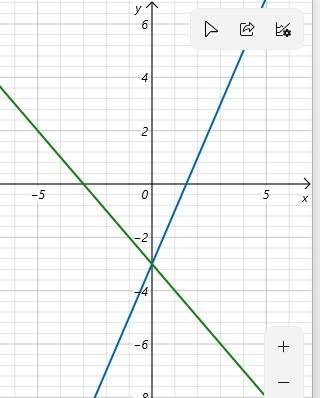
Giao của d1 và d2 là điểm có hoành độ thỏa mãn phương trình 

       2\(x\) - 3 = -3 - \(x\)

      2\(x\) + \(x\) = 0 

          3\(x\) =0 

            \(x\) = 0

    ⇒ y = -3 - 0 

       y = - 3

Vậy giao của d1 và d2 là điểm B(0; -3)

a: Xét ΔAHD có 

AP là đường cao ứng với cạnh HD

AP là đường trung tuyến ứng với cạnh HD

Do đó: ΔAHD cân tại A

mà AP là đường cao ứng với cạnh HD

nên AP là đường phân giác ứng với cạnh HD

Xét ΔAHE có 

AQ là đường cao ứng với cạnh HE

AQ là đường trung tuyến ứng với cạnh HE

Do đó: ΔHAE cân tại A

mà AQ là đường cao ứng với cạnh HE

nên AQ là đường phân giác ứng với cạnh HE

Ta có: \(\widehat{EAD}=\widehat{EAH}+\widehat{DAH}\)

\(=2\left(\widehat{QAH}+\widehat{PAH}\right)\)

\(=2\cdot90^0=180^0\)

Do đó: E,A,D thẳng hàng

mà AD=AE(=AH)

nên A là trung điểm của DE

a) Xét \(\Delta ADP\) = \(\Delta AHP\) có: ( cạnh huyền -cạnh góc vuông)

góc APD = APH=90o

AD = AH

AP chung                                               

=> AD=AH (1)

CMTT với \(\Delta AEQ=\Delta AHQ\left(CH-CGV\right)\)

=> AE= AH (2)

Từ 1 và 2 => AD= AE

=> A là trung điểm của DE

b) Xét \(\Delta DHE\) có:

DP=PH; HQ=QE

=> PQ là đg trung bình của tam giắc DHE

=> PQ// DE; PQ=1/2 DE

c) Xét tứ giác APHQ có: góc HPA= 90o; Góc A =90o; góc HQA=90o 

=> Tứ giác APHQ là HCN

=> PQ=AH ( theo t/c HCN)  

a: Xét ΔABC có 

BD là đường cao

CE là đường cao

BD cắt CE tại H

Do đó: H là trực tâm của ΔABC

hay AM⊥BC

Xét ΔAEC vuông tại E và ΔADB vuông tại D có

góc EAC chung

Do đó: ΔAEC\(\sim\)ΔADB

b: Xét ΔAED và ΔACB có

AE/AC=AD/AB

góc EAD chung

Do đó: ΔAED\(\sim\)ΔACB