- Với \(xy=0\Rightarrow P=1\)

- Với \(xy\ne0\):

Bình phương giả thiết:

\(4x^{2012}y^{2012}=\left(x^{2013}+y^{2013}\right)^2\ge4x^{2013}y^{2013}\)

\(\Rightarrow4x^{2012}y^{2012}\left(1-xy\right)\ge0\)

\(\Rightarrow1-xy\ge0\)

\(\Rightarrow P_{min}=0\) khi \(x=y=1\)

Dễ này á anh ;;-;;

Lời giải:

Lấy PT(1) cộng với 2 lần PT (2) ta được:

$x+2y+2(2x-y)=3m+4+2(m+3)$

$\Leftrightarrow 5x=5m+10$

$\Leftrightarrow x=m+2$
Khi đó: $y=2x-(m+3)=2m+4-m-3=m+1$

Vậy HPT có nghiệm $(x,y)=(m+2, m+1)$

$x,y$ là độ dài tam giác cân có cạnh huyền, tức là tam giác vuông cân.

Trong tam giác vuông cân chỉ có 1 cạnh huyền và 2 cạnh còn lại bằng nhau và là cạnh góc vuông. Vì $m+2\neq m+1$ nên 1 trong 2 số này sẽ không phải độ dài cạnh góc vuông. 

Hiển nhiên $m+2> m+1$ nên $m+2$ là độ dài cạnh huyền.

$\Rightarrow m+2=\sqrt{5}$
$\Rightarrow m=\sqrt{5}-2$

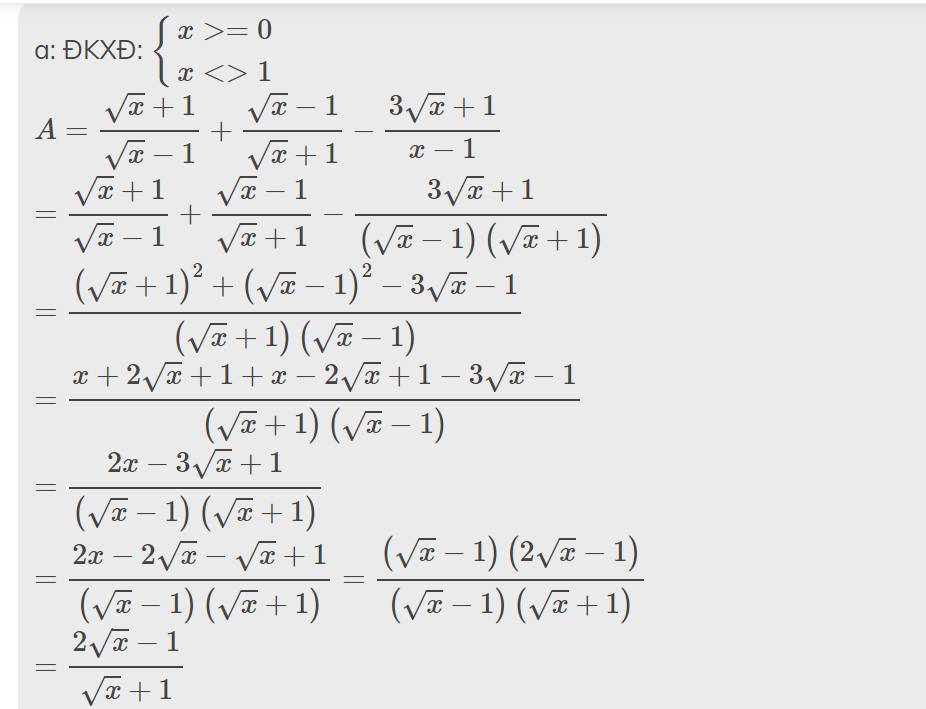
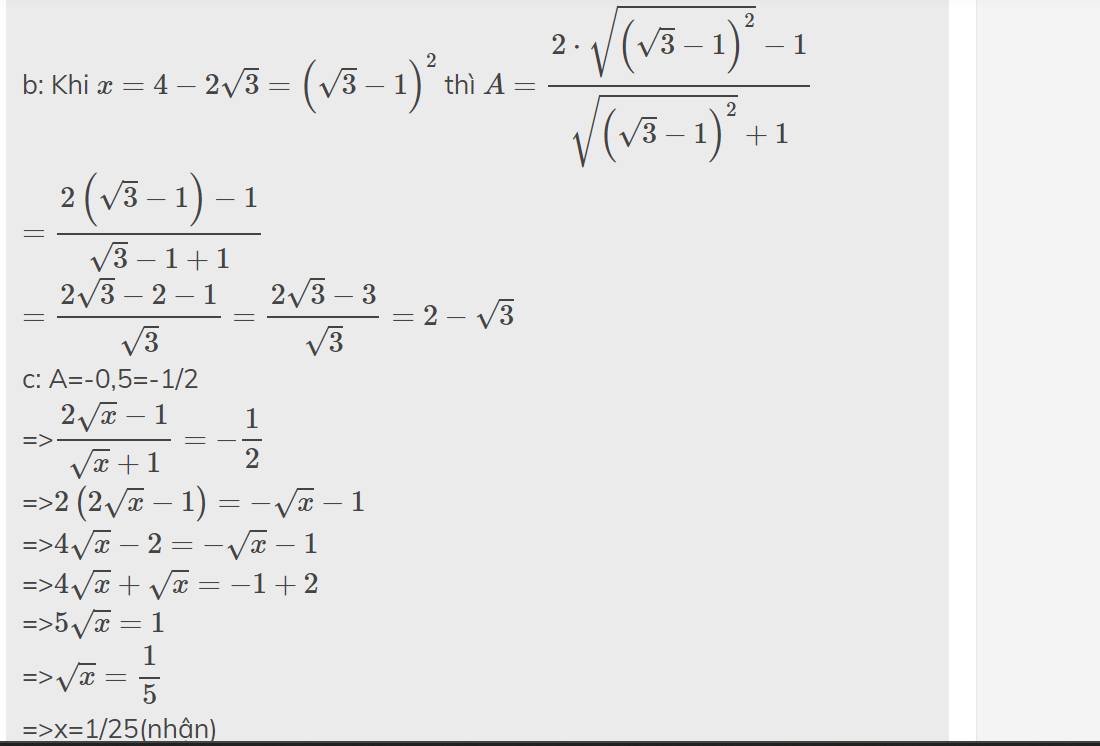
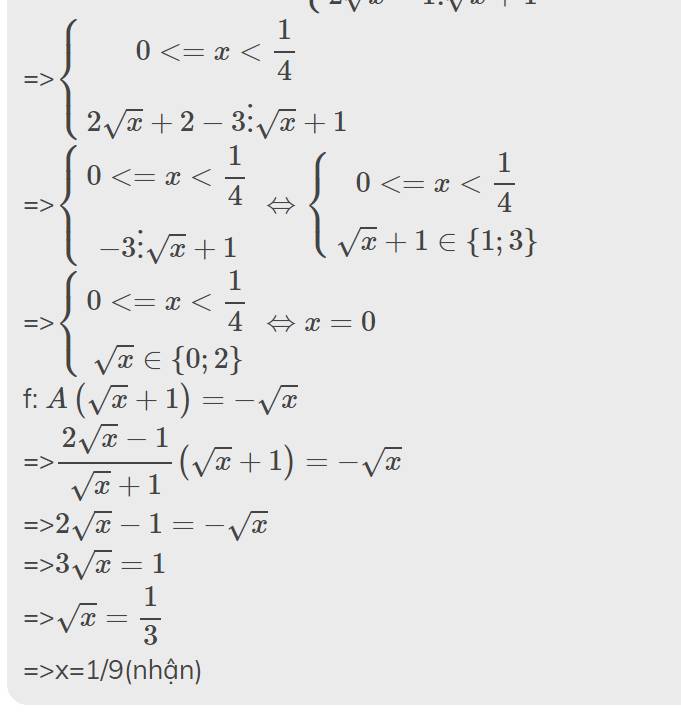
g: A<1

=>\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\)

=>\(\dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\)

=>\(\sqrt{x}-2< 0\)

=>\(\sqrt{x}< 2\)

=>0<=x<4

Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< =x< 4\\x< >1\end{matrix}\right.\)

h: \(A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)

=>\(A=\dfrac{2\sqrt{x}+2-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\)

\(\sqrt{x}+1>=1\forall x\) thỏa mãn ĐKXĐ

=>\(\dfrac{3}{\sqrt{x}+1}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ

=>\(-\dfrac{3}{\sqrt{x}+1}>=-3\forall x\) thỏa mãn ĐKXĐ

=>\(-\dfrac{3}{\sqrt{x}+1}+2>=-3+2=-1\forall x\) thỏa mãn ĐKXĐ

=>\(A>=-1\forall x\) thỏa mãn ĐKXĐ

Vậy: \(A_{min}=-1\) khi x=0

i: \(P=A\left(-x+2\sqrt{x}+3\right)\)

\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\cdot\left(-1\right)\cdot\left(x-2\sqrt{x}-3\right)\)

\(=\dfrac{1-2\sqrt{x}}{\sqrt{x}+1}\cdot\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)\)

\(=\left(1-2\sqrt{x}\right)\left(\sqrt{x}-3\right)\)

\(=\sqrt{x}-3-2x+6\sqrt{x}=-2x+7\sqrt{x}-3\)

\(=-2\left(x-\dfrac{7}{2}\sqrt{x}+\dfrac{3}{2}\right)\)

\(=-2\left(x-2\cdot\sqrt{x}\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{1}{16}\right)\)

\(=-2\left(\sqrt{x}-\dfrac{7}{4}\right)^2+\dfrac{1}{8}< =\dfrac{1}{8}\forall x\) thỏa mãn ĐKXĐ

Dấu '=' xảy ra khi \(\sqrt{x}-\dfrac{7}{4}=0\)

=>\(\sqrt{x}=\dfrac{7}{4}\)

=>\(x=\dfrac{49}{16}\)

1: Xét ΔMNP vuông tại M có MH là đường cao

nên MH^2=HN*HP; MN^2=NH*NP; PM^2=PH*PN

=>MH=căn 3,6*6,4=4,8cm; MN=căn 3,6*10=6cm; PM=căn 6,4*10=8cm

2: MK=8/2=4cm

Xét ΔMNK vuông tại M có tan MNK=MK/MN=4/6=2/3

nên \(\widehat{MNK}\simeq33^041'\)

3: ΔMNK vuông tại M có MF là đường cao

nên NF*NK=NM^2

ΔMNP vuông tại M có MH là đường cao

nên NH*NP=NM^2

=>NF*NK=NH*NP

a) \(\sqrt[]{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)

\(\Leftrightarrow\sqrt[]{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+9}=-\left(x^2+2x+1\right)+5\)

\(\Leftrightarrow\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}=-\left(x+1\right)^2+5\left(1\right)\)

Ta có :

\(\left\{{}\begin{matrix}\sqrt[]{3\left(x+1\right)^2+4}\ge2,\forall x\in R\\\sqrt[]{5\left(x+1\right)^2+9}\ge3,\forall x\in R\end{matrix}\right.\)

\(\Rightarrow VT=\sqrt[]{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge5,\forall x\in R\)

\(VP=-\left(x+1\right)^2+5\le5,\forall x\in R\)

Dấu "=" xảy ra thì \(VT=VP=5\)

\(\left(1\right)\Leftrightarrow\left(x+1\right)^2=0\)

\(\Leftrightarrow x+1=0\)

\(\Leftrightarrow x=-1\)

Vậy nghiệm của phương trình đã cho là \(x=-1\)

a: ΔOHB cân tại O

mà OI là đường trung tuyến

nên OI\(\perp\)HB

I là trung điểm của HB

=>\(IH=IB=\dfrac{HB}{2}=\dfrac{8}{2}=4\left(cm\right)\)

ΔOIB vuông tại I

=>\(OB^2=OI^2+IB^2\)

=>\(OB^2=3^2+4^2=25\)

=>OB=5(cm)

=>R=5(cm)

Xét tứ giác MAOI có

\(\widehat{MAO}+\widehat{MIO}=90^0+90^0=180^0\)

=>MAOI là tứ giác nội tiếp đường tròn đường kính MO

Tâm là trung điểm của MO

b: Xét (O) có

ΔAHB nội tiếp

AB là đường kính

Do đó; ΔAHB vuông tại H

=>AH\(\perp\)HB tại H

=>AH\(\perp\)MB tại H

Xét ΔMAB vuông tại A có AH là đường cao

nên \(MA^2=MH\cdot MB\)

c: Xét (O) có

MA,MK là tiếp tuyến

Do đó: MA=MK

mà OA=OK

nên MO là đường trung trực của AK

\(MA^2=MH\cdot MB\)

MA=MK

Do đó: \(MK^2=MH\cdot MB\)

=>\(\dfrac{MK}{MH}=\dfrac{MB}{MK}\)

Xét ΔMKB và ΔMHK có

\(\dfrac{MK}{MH}=\dfrac{MB}{MK}\)

\(\widehat{KMB}\) chung

Do đó: ΔMKB đồng dạng với ΔMHK

=>\(\widehat{MBK}=\widehat{MHK}\)

a: Vì y=ax+5//y=2x nên ta có:

\(\left\{{}\begin{matrix}a=2\\b< >0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}a=2\\5< >0\left(đúng\right)\end{matrix}\right.\)

=>a=2

b: Thay x=-1 và y=3 vào y=x+b, ta được:

\(b-1=3\)

=>b=1+3=4

Vậy: b=4

c: (d1): y=2x+5

(d2): y=x+4

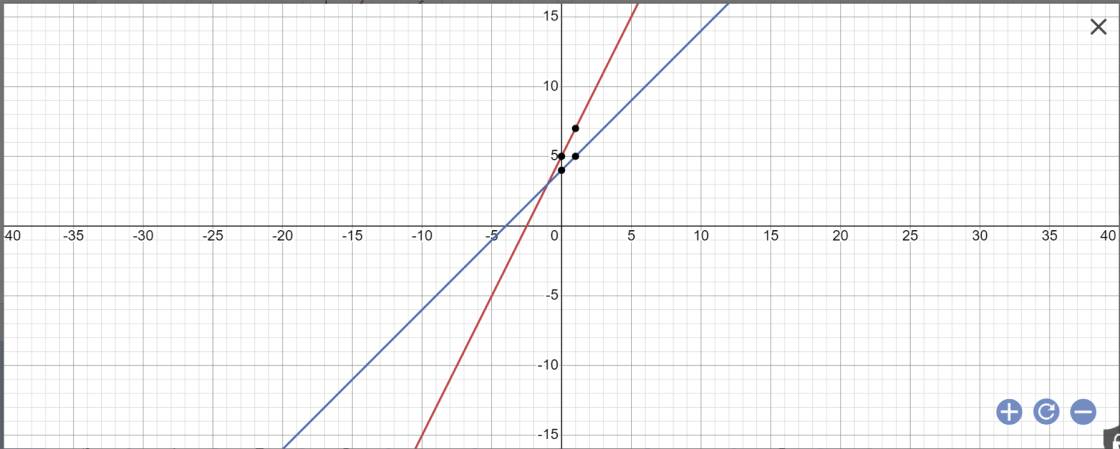
c: tọa độ điểm C là:

\(\left\{{}\begin{matrix}2x+5=x+4\\y=x+4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-x=4-5\\y=x+4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-1\\y=-1+4=3\end{matrix}\right.\)

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-\dfrac{5}{2}\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}y=0\\x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=0-4=-4\end{matrix}\right.\)

vậy:B(-4;0); C(-5/2;0); A(-1;3)

d: \(BC=\sqrt{\left(-\dfrac{5}{2}+4\right)^2+\left(0-0\right)^2}=1,5\)

\(BA=\sqrt{\left(-1+4\right)^2+\left(3-0\right)^2}=\sqrt{3^2+3^2}=3\sqrt{2}\)

\(AC=\sqrt{\left(-\dfrac{5}{2}+1\right)^2+\left(0-3\right)^2}=\sqrt{\left(-1,5\right)^2+\left(-3\right)^2}=\dfrac{3\sqrt{5}}{2}\)

Chu vi tam giác ABC là: 

\(C_{ABC}=AB+BC+AC=1,5+3\sqrt{2}+\dfrac{3\sqrt{5}}{2}\)

Xét \(\Delta\)ABC có 

\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{18+11,25-2,25}{2\cdot3\sqrt{2}\cdot\dfrac{3\sqrt{5}}{2}}=\dfrac{27}{9\sqrt{10}}=\dfrac{3}{\sqrt{10}}\)

=>\(sinBAC=\sqrt{1-cos^2BAC}=\dfrac{1}{\sqrt{10}}\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot3\sqrt{2}\cdot\dfrac{3\sqrt{5}}{2}\cdot\dfrac{1}{\sqrt{10}}=\dfrac{9}{4}\)

a: Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(AH^2=4\cdot9=36\)

=>\(AH=\sqrt{36}=6\left(cm\right)\)

b: Xét (O) có

ΔAEH nội tiếp

AH là đường kính

Do đó; ΔAEH vuông tại E

=>HE\(\perp\)AE tại E

=>HE\(\perp\)AB tại E

Xét (O) có

ΔAFH nội tiếp

AH là đường kính

Do đó; ΔAFH vuông tại F

=>HF\(\perp\)FA tại F

=>HF\(\perp\)AC tại F

Xét tứ giác AEHF có

\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)

=>AEHF là hình chữ nhật

c: Ta có: ΔHEB vuông tại E

mà EM là đường trung tuyến

nên EM=HM

=>\(\widehat{MHE}=\widehat{MEH}\)

mà \(\widehat{MHE}=\widehat{ACB}\)(hai góc đồng vị, HE//AC)

nên \(\widehat{MEH}=\widehat{ACB}\)

Ta có: AEHF là hình chữ nhật

=>\(\widehat{FEH}=\widehat{FAH}\)

mà \(\widehat{FAH}=\widehat{ABC}\left(=90^0-\widehat{HCA}\right)\)

nên \(\widehat{FEH}=\widehat{ABC}\)

\(\widehat{MEF}=\widehat{MEH}+\widehat{FEH}\)

\(=\widehat{ABC}+\widehat{ACB}=90^0\)

Vì AEHF là hình chữ nhật

nên AEHF nội tiếp đường tròn đường kính AH và EF

=>EF là đường kính của (O)

Xét (O) có

EF là đường kính

EM\(\perp\)EF tại E

=>EM là tiếp tuyến của (O)