Bằng phản chứng giả sử a và b đều âm 

\(\Rightarrow a< 0,b< 0\Rightarrow a+b< 0\)

Mà theo đề: \(a+b>0\)---> Mâu thuẫn giả thiết, vậy có ít nhất 1 trong a,b phải dương

a. a dương => a > 0; a \(\in\) Z⁺

Số liền sau của a là : a + 1

Mà 1 > 0; 1 \(\in\) Z⁺ => a + 1 > 0; a + 1 \(\in\) Z⁺

=>  Nếu a dương thì số liền sau a cũng dương.

b. a âm => a < 0; a \(\in\) Z^-

Số liền trước của a là: a - 1

Mà -1 < 0; -1 \(\in\) Z^- => a - 1 < 0; a - 1 \(\in\) Z^-

=>  Nếu a âm thì số liền trước a cũng âm.

c. Kết luận: Số liền sau của 1 số dương là 1 số dương, số liền trước của 1 số âm là 1 số âm.

a.a  dương => a > 0; a\(\in\) 2

Số liền sau của a là : a + 1

Mà 1 > 0; 1 \(\in\) Z⁺ => a + 1 > 0; a + 1 \(\in\) Z⁺

=> Nếu a dương thì số liền sau a cũng dương

b.a âm => a < 0; a\(\in\) Z

Số liền trước của a là : a - 1

Mà - 1 < 0; - 1 < 0; a - 1 \(\in\) Z

=> Nếu a âm thì số liền trước a cũng âm

c.Kết luận : Số liền sau của 1 số dương thì 1 số dương:số liền trước của 1 số âm thì 1 số âm

Tham khảo:

Gỉa sử : a+b+c> 1/a + 1/b + 1/c nhưng không thỏa mãn một và chỉ một trong 3 số a,b,c lớn hơn 1

*TH1:Cả 3 số a,b,c đều lớn hơn 1 hoặc đều nhỏ hơn 1 suy ra mâu thẫn( vì abc=1)

*TH2: có 2 số lớn hơn 1

Gỉa sử: a>1, b>1, c<1 <=> a-1>0 , b-1>0 , c-1<0

=> (a-1)(b-1)(c-1)<0 

=>abc+a+b+c-(ab+bc+ca)-1<0

<=>a+b+c<ab+bc+ca 

<=>a+b+c<abc/c+abc/a+abc/b 

Thay abc=1 ta được:

a+b+c<1/a+1/b+1/c(mâu thuẫn với giả thuyết nên điều giả sử sai)

=>đpcm

 Trường hợp 1: Giả sử ba số $a$, $b$, $c$ đều lớn hơn $1$ hoặc ba số $a$, $b$, $c$ đều nhỏ hơn $1$.

Khi đó a.b.c \ne 1
 a.b.c $\ne 1$ (trái với giả thiết).

 Trường hợp 2: Giả sử hai trong ba số $a$, $b$, $c$ lớn hơn 1.

Không mất tính tổng quát, giả sử $a>1$ và $b>1$.

Vì $a.b.c=1$ nên $c\; <1$ do đó:

     $(a-1).(b-1).(c-1)<0$

$\iff abc+a+b+c-ab-ac-ca-1<0$

$\iff a+b+c-ab-ac-ca<0$

$\iff a+b+c<ab+ac+ca$

$\iff$a + b + c < $\backslash (\backslash dfrac\{abc\}\{c\}\backslash )$ + \(\dfrac{abc}{a}\) + \(\dfrac{abc}{b}\)

⇔ a + b + c < \(\dfrac{1}{c}\) + \(\dfrac{1}{a}\) + \(\dfrac{1}{b}\) (mâu thuẫn với giả thiết)

Vậy chỉ có một và chỉ một trong ba số $a$, $b$, $c$ lớn hơn $1$

Giả sử 99 số đó đều không lớn hơn 1

Đặt \(a_1\le a_2\le a_3\le...\le a_{99}\le11\)

Lúc đó: \(a_1+a_2+a_3+...+a_{99}\le99< 100\)

Vậy điều giả sử là sai. 

Suy ra được:  Nếu tổng của 99 số bằng 100 thì có ít nhất 1 số lớn hơn 1.

Tham khảo:

Dễ thấy: \(\overrightarrow u .\;\overrightarrow v \) cùng dấu với \(\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\) (do \(\left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| > 0\)). Do đó:

+) \(\overrightarrow u .\;\overrightarrow v \;\; > 0\)  \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) > 0\) hay \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\)

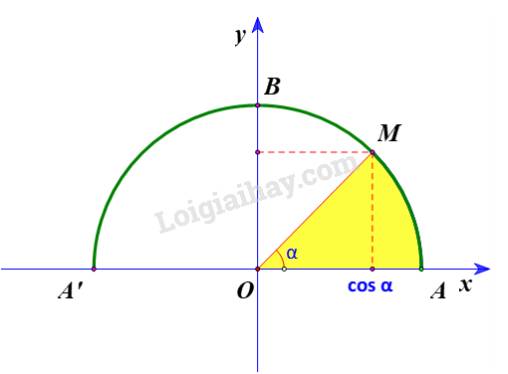
+) \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) \( \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\;\; < 0\) hay \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}\)

Vậy \(\overrightarrow u .\;\overrightarrow v \;\; > 0\)  nếu \({0^o} \le \left( {\overrightarrow u ,\;\overrightarrow v } \right) < {90^o}\) và \(\overrightarrow u .\;\overrightarrow v \;\; < 0\) nếu \({90^o} < \left( {\overrightarrow u ,\;\overrightarrow v } \right) \le {180^o}.\)

1, Đúng

2, Sai ( VD \(\sqrt{3^2}⋮3\) nhưng \(\sqrt{3}⋮̸3\))

-----------HẾT----------------

1/ Giả sử n là số chẵn : 2k

\(\Rightarrow n^2=4k^2\)

Mà 4k² chẵn (trái vs gt)

=> đpcm

2/Giả sử \(n⋮̸\) 3

\(\Rightarrow n.n⋮̸\) 3

\(\Leftrightarrow n^2⋮̸\) 3(trái gt)

=> đpcm

3/ Giả sử \(a+b< 2\sqrt{ab}\Leftrightarrow a-2\sqrt{ab}+b< 0\)

\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2< 0\) (vô lí)

=> đpcm

4/ Giả sử \(x\ne0\Rightarrow x^2\ne0;y\ne0\Rightarrow y^2\ne0\)

\(\Rightarrow x^2+y^2\ne0\) (trái gt)

=> đpcm

Câu 5 bn xem lại đề bài nhé vì nếu x=y=-2 thì x+y+xy= 0\(\ne-1\)

6/ Gọi 2 số thực là a và b

Giả sử \(a=1;b=1\Rightarrow a+b=2\) (trái gt)

=> đpcm

ko thì bn giả sử \(a< 1;b< 1\Rightarrow a+b< 2\) (trái gt) cũng đc

P/s: mk ms hok dạng này nên có sai sót j xin rộng lượng bỏ qua. Đa tạ!