
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là C
Số cách chọn 2 số chẵn trong tập hợp 2 ; 4 ; 6 ; 8 là: C 4 2 cách.
Số cách chọn 2 số lẻ trong tập hợp 1 ; 3 ; 5 ; 7 ; 9 là: C 5 2 cách.
Số cách hoán vị 4 chữ số đã chọn lập thành 1 số tự nhiên là: 4! cách.
Vậy có 4 ! . C 4 2 . C 5 2 số tự nhiên thỏa mãn yêu cầu bài toán.

Chọn 2 số lẻ từ 5 chữ số lẻ: \(C_5^2\)
Chọn 3 chữ số chẵn từ 5 chữ số chẵn: \(C_5^3\)
Xếp 8 chữ số theo thứ tự bất kì: \(C_5^2.C_5^3.\dfrac{8!}{2!.2!.2!}\)
Chọn 3 chữ số chẵn từ 5 chữ số chẵn trong đó có mặt số 0: \(C_4^2\)
Xếp 8 chữ số (có mặt số 0) sao cho số 0 đứng đầu: \(C_5^2C_4^2.\dfrac{7!}{2!.2!}\)
Số số thỏa mãn: \(C_5^2C_5^2\dfrac{8!}{2!.2!.2!}-C_5^2C_4^2.\dfrac{7!}{2!.2!}=...\)
Đưa các chữ số của số tự nhiên cần lập vào các ô trống:
| . | . | . | . | . | . | . | . |
TH1: Có chữ số 0:
Đưa 0 vào : \(C^2_7\) cách
Chọn và đưa 2 số chẵn còn lại vào : \(C^2_4C^2_6C^2_4\) cách
Chọn 2 chữ số lẻ : \(A^2_5\) cách
=>TH1 lập được \(C^2_7C^2_4C^2_6C^2_4A^2_5=226800\) số
TH2: Không có chữ số 0:
Chọn và đưa 3 số chẵn vào : \(C^3_4C^2_8C^2_6C^2_4\) cách
Chọn 2 chữ số lẻ : \(A^2_5\) cách
=>TH2 lập được \(C^3_4C^2_8C^2_6C^2_4A^2_5=201600\) số
Vậy có 226800 + 201600 = 428400 số

TH1: chữ số hàng đơn vị bằng 0
Chọn 4 chữ số từ 8 chữ số còn lại và hoán vị chúng: \(A_8^4\) cách
4 chữ số này tạo ra 5 khe trống, xếp 3 chữ số 1 vào 5 khe trống đó: \(C_5^3\) cách
\(\Rightarrow A_8^4.C_5^3\) số
TH2: chữ số hàng đơn vị khác 0: có 4 cách chọn
- Chọn 4 chữ số từ 8 chữ số còn lại và hoán vị chúng: \(A_8^4\) cách
Xếp 3 chữ số 1 vào 5 khe trống: \(C_5^3\) cách
- Chọn 4 chữ số từ 8 chữ số còn lại sao cho có xuất hiện số 0, cố định số 0 đứng đầu và hoán vị 3 chữ số còn lại: \(A_7^3\) cách
3 chữ số tạo ra 4 khe trống, xếp 3 chữ số 1 vào 4 khe trống: \(C_4^3\) cách
\(\Rightarrow4\left(A_8^4.C_5^3-A_7^3.C_4^3\right)\) số
Tổng cộng: \(A_8^4.C_5^3+4\left(A_8^4.C_5^3-A_7^3.C_5^3\right)\) số
Cho mình hỏi là cái chỗ "4 chữ số này tạo ra 5 khe trống" là sao thế ạ

Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: 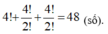
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: 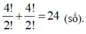
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: 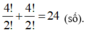
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: 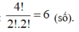
Vậy có thể lập được 102 số thỏa mãn đề bài.

3:
Ta sẽ chia M ra làm 3 nhóm
Nhóm 1: \(A=\left\{0;3;6\right\}\)
Nhóm 2: \(B=\left\{1;4;7\right\}\)
Nhóm 3: \(C=\left\{2;5;8\right\}\)
TH1: 1 số A,1 số B, 1 số C
*Nếu số ở A chọn là số 0 thì sẽ có 3*3*2*2*1=36 cách
*Nếu số A chọn khác 0 thì sẽ là 2*3*3*3!=108 cách
=>Có 108+36=144 cách
TH2: 3 số A
=>Có 2*2*1=4 số
TH3: 3 số B
=>Có 3!=6 số
TH4: 3 số C
=>Có 3!=6 số
=>Có 144+4+6+6=148+12=160 số

\(\overline{abcde}\).
- TH1 : a là số chẵn ⇒ Giả sử b,c là số chẵn và d,e là số lẻ
+ Chọn số cho a có 4 cách (2 ; 4 ; 6 ; 8) : Lưu ý là chữ số đầu tiên của số có từ 2 chữ số trở nên không được là số 0
+ Chọn số cho b có 3 cách
+ Chọn số cho c có 2 cách
+ Chọn số cho d có 5 cách
+ Chọn số cho e có 4 cách
⇒ Nếu a là số chẵn thì sẽ có 4 . 3 . 2 . 5 . 4 = 480 số
- Nếu a là số lẻ, giả sử b là số lẻ và c,d,e là số chẵn
+ Chọn số cho a có 5 cách
+ Chọn số cho b có 4 cách
+ Chọn số cho c có 5 cách
+ Chọn số cho d có 4 cách
Chọn số cho e có 3 cách
Vậy khi a là số lẻ thì có 5 . 4 . 5 . 4 . 3 = 1200 (số)
Vậy rốt cuộc là có 1200 + 480 = 1680 (số)