
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Mình nghĩ là không tồn tại , số chính phương hay ta có thể gọi nó là lũy thừa căn bậc 2 của 1 số , mà đây ta có các chữ số đều giống nhau , không thể thực hiên .
Các chữ số giống nhau nên nếu a có tồn tại thì a sẽ là các chữ số từ 1 - 9 ( a không thể là 0 )
mà các số đều dư khi sử dụng căn bậc \(\sqrt{ }\)
nên không có bất cứ số a nào thỏa mãn đề bài

Hỏi mấy bạn chuyên lí đi dễ mà: đặt ẩn x là vận tốc thực của thuyền (x>4)
=> gpt thời gian : ( thời gian bè trôi và thuyền chạy đến điểm gặp là như nhau)
(24/x+4)+(24-8/x-4)=8/4 => x= tự bấm máy ( lười vì đang giải bài trên giường)

Áp dụng BĐT Cô-si dạng Engel,ta có :
\(P=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{a^2+b^2+c^2}=a^2+b^2+c^2\)
\(3\left(a^2+b^2+c^2\right)\ge\left(a+b+c\right)^2\Rightarrow\sqrt{3\left(a^2+b^2+c^2\right)}\ge a+b+c\)
\(\Rightarrow6=a+b+c+ab+bc+ac\le\sqrt{3\left(a^2+b^2+c^2\right)}+a^2+b^2+c^2\)
Đặt \(\sqrt{3\left(a^2+b^2+c^2\right)}=t\Rightarrow a^2+b^2+c^2=\frac{t^2}{3}\)
\(\Rightarrow t+\frac{t^2}{3}\ge6\Leftrightarrow3t+t^2-18\ge0\Leftrightarrow\left(t-3\right)\left(t+6\right)\ge0\)
\(\Rightarrow t-3\ge0\Rightarrow t\ge3\)( vì t + 6 > 0 )
\(\Rightarrow P\ge a^2+b^2+c^2=\frac{t^2}{3}\ge3\)
Vậy GTNN của P là 3 khi a = b = c = 1
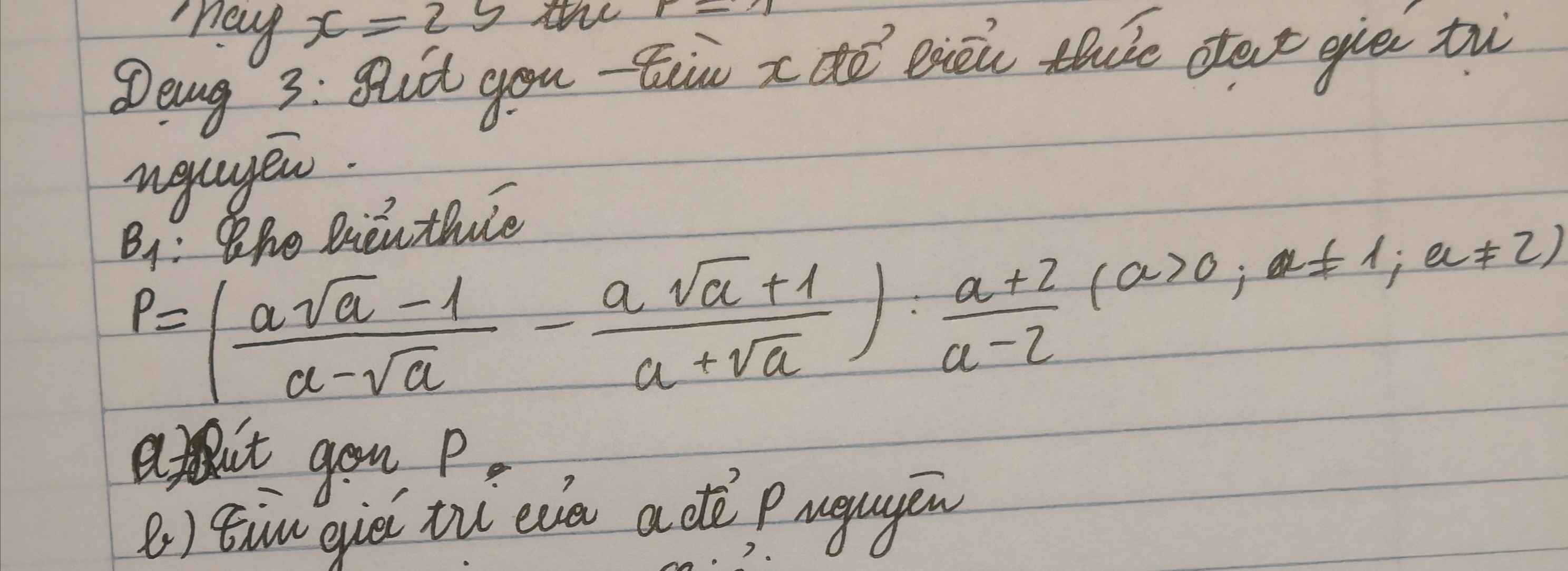
a: Ta có: \(P=\left(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\dfrac{a+2}{a-2}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}\cdot\dfrac{a-2}{a+2}\)
\(=\dfrac{2a-4}{a+2}\)