Gọi khối lượng mỗi quặng là a và b (tấn)

ta có: \(\frac{70a+40b}{a+b}=60\Leftrightarrow\frac{30a}{a+b}+40=60\Leftrightarrow30a=20\left(a+b\right)\Leftrightarrow10a=20b\Leftrightarrow a=2b\)

lại có\(\frac{70\left(a-8\right)+40\left(b-2\right)}{\left(a-8\right)+\left(b-2\right)}=58\Leftrightarrow\frac{30\left(a-8\right)}{a-8+b-2}+40=58\Leftrightarrow30\left(a-8\right)=18\left(a+b-10\right)\)

\(\Leftrightarrow30a-240=18a+18b-180\Leftrightarrow12a-18b=60\)

thay a=2b vào phương trình trên ta có

\(12\times2b-18b=60\Leftrightarrow24b-18b=60\Leftrightarrow6b=60\Leftrightarrow b=10\Rightarrow a=20\)

Vậy khối lượng quặng 1 là 20 tấn, khối lượng quặng 2 là 10 tấn

Gọi khối lượng quặng loại thứ nhất là x ( tấn), loại thứ hai là y (tấn)

Điều kiện: x > 0; y > 0

Lượng sắt nguyên chất có trong mỗi loại quặng bằng lượng sắt có trong hỗn hợp ta có phương trình:

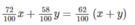
Thêm mỗi loại quặng 15 tấn ta được hỗn hợp chứa 63,25% sắt, ta có phương trình:

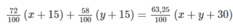
Ta có hệ phương trình:

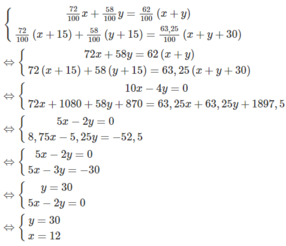
Cả hai giá trị x = 12; y = 30 thỏa mãn điều kiện bài toán.

Vậy loại quặng thứ nhất có 12 tấn, loại quặng thứ hai có 30 tấn.

Gọi khối lượng quặng loại thứ nhất là x tấn ,loại thứ 2 là y tấn ,x>0 ; y>0

ta có hệ phương trình :\(\hept{\frac{\frac{72}{100}x+\frac{58}{100}y=\frac{62}{100}\left(x+y\right)}{\frac{72}{100}\left(x+15\right)+\frac{58}{100}\left(y+15\right)=\frac{63,25}{100}\left(x+y+30\right)}}\)

hay : \(\hept{\begin{cases}5x-2y=0\\5\left(x+15\right)=3\left(y+15\right)\end{cases}}\)

giải hệ phương trình ta đc: (x;y) =(12;30)

vậy khối lượng loại thứ nhất là 12 tấn , loai thứ 2 là 30 tấn

Để cho ra quặng 66% thì cần trộn tỷ lệ quặng 75% : quặng 50% là 82/75 : 1 hay 82/75 : 75/75.
Như vậy để có 25 tấn quặng 66% thì cần:
Quặng 75%
(82 x 25) : (82 + 75)= 2075/157 tấn
Quặng 50%
(75 x25) :(82+75)= 1875/157 tấn

Gọi khối lượng của quặng loại I là x(tấn)

(Điều kiện: 0<x<=10)

Khối lượng của quặng loại II là 10-x(tấn)

Tỉ lệ sắt nguyên chất trong quặng loại I là \(\dfrac{0.8}{x}\left(tấn\right)\)

Tỉ lệ sắt nguyên chất trong quặng loại II là \(\dfrac{0.6}{10-x}\left(tấn\right)\)

Tỉ lệ sắt nguyên chất trong quặng loại I nhiều hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10%=0,1 nên ta có;

\(\dfrac{0.8}{x}-\dfrac{0.6}{10-x}=0.1\)

=>\(\dfrac{8}{x}-\dfrac{6}{10-x}=1\)

=>\(\dfrac{8}{x}+\dfrac{6}{x-10}=1\)

=>\(\dfrac{8x-80+6x}{x\left(x-10\right)}=1\)

=>\(x\left(x-10\right)=14x-80\)

=>\(x^2-24x+80=0\)

=>(x-20)(x-4)=0

=>\(\left[{}\begin{matrix}x-20=0\\x-4=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=20\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)

Vậy: Khối lượng quặng loại I là 4 tấn

Khối lượng quặng loại II là 10-4=6 tấn