Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi M x 0 ; y 0 ∈ C ⇒ y ' x 0 = 3 x 0 2 - 3 và y x 0 = x 0 3 - 3 x 0 .
Suy ra phương trình tiếp tuyến của (C) tại M là y = y x 0 = y ' x 0 . x - x 0 .
⇔ y = 3 x 0 2 - 3 . x - x 0 + x 0 3 - 3 x 0 = 3 x 0 2 - 3 . x - 2 x 0 3 ( d ) .
Phương trình hoành độ giao điểm của (C) và (d) là x 3 - 3 x = 3 x 0 2 - 3 x - 2 x 0 3
⇔ x 3 - 3 x 0 2 . x + 2 x 0 3 = 0 ⇔ x - x 0 2 x + 2 x 0 = 0 ⇔ [ x = x 0 x = - 2 x 0 .
Vậy x M = x 0 x N = - 2 x 0 ⇒ 2 x M + x N = 0 .

Gọi ![]()
phương trình tiếp tuyến của (C) tại M là
![]()
Phương trình hoành độ giao điểm:
![]()
![]()
![]()
![]()
Yêu cầu bài toán tương đương với (1) có hai nghiệm phân biệt khác
![]()
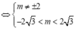
![]()
Vậy có tất cả 5 điểm có toạ độ nguyên thoả mãn.
Chọn đáp án A.

Chọn D
Đặt M(a;b;c). Điểm M thuộc mặt phẳng (P) ta được phương trình 2a-b-c+4=0. Hai phương trình còn lại từ giả thiết MA=MA, MA=3

Đáp án A
Gọi M a ; a 3 − 3 a suy ra PTTT tại M là: y = 3 a 2 − 3 x − a + a 3 − 3 a d
Ta có:
d ∩ Ox = B − a 3 + 3 a 3 a 2 − 3 + a ; 0
Phương trình hoành độ giao điểm của d và C là :
x 3 − 3 x = 3 a 2 − 3 x − a + a 3 − 3 a
⇔ x − a x 2 + ax + a 2 − 3 x − a = 3 a 2 − 3 x − a ⇔ x − a x 2 + a x − 2 a 2 = 0 ⇔ x − a 2 x + 2 a = 0 ⇔ x = − 2 a ⇒ A − 2 a ; − 8 a 3 + 6 a
Do A, M, B luôn thuộc tiếp tuyến d nên để M là trung điểm của AB thì:
2 y M = y A + y B
⇔ 2 a 3 − 6 a = − 8 a 3 + 6 a ⇔ 10 a 3 = 12 a ⇔ a = 0 a = ± 6 5
Do M ≠ 0 ⇒ a ≠ 0 ⇒ a = ± 6 5 .
Vậy có 2 điểm M thỏa mãn yêu cầu.




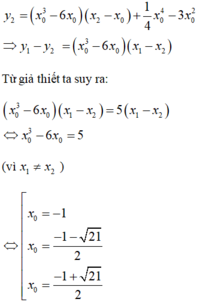

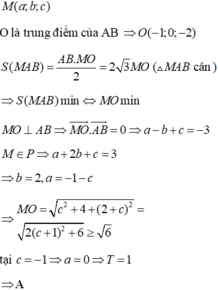
không có vì nếu a/b=a.m/b.n thì chia 2 vế cho a/b ta được 1=m/n hay m=n (trái giả thiết)