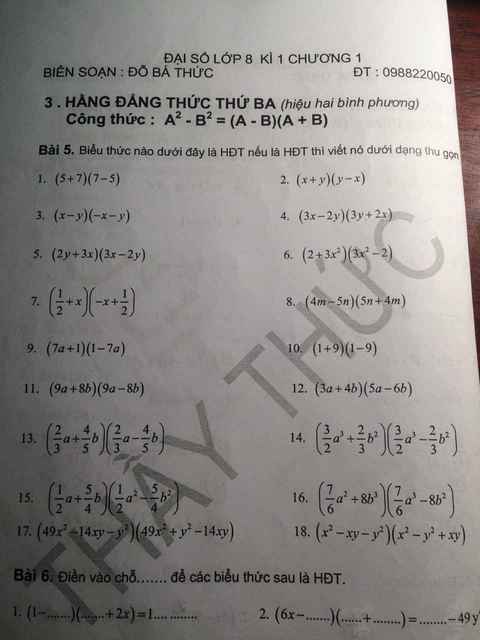Giải:

1) \(a^3-3a^2+3a-1\)

\(=a^3-3a^2.1+3a.1^2-1^3\)

\(=\left(a-1\right)^3\)

Vậy ...

2) \(x^3+6x^2+12x+8\)

\(=x^3+3.x^2.2+3.x.2^2+2^3\)

\(=\left(x+2\right)^3\)

Vậy ...

3) \(8x^3-12x^2+6x-1\)

\(=\left(2x\right)^3-3.\left(2x\right)^2.1+3.2x.1^2-1^3\)

\(=\left(2x-1\right)^3\)

Vậy ...

4) \(x^3-6x^2y+12xy^2-8y^3\)

\(=x^3-3.x^2.2y+3.x.\left(2y\right)^2-\left(2y\right)^3\)

\(=\left(x-2y\right)^3\)

Vậy ...

tách nhỏ ra đi ak

Bài 5:

1) \(\left(5+7\right)\left(7-5\right)=7^2-5^2\)

2) \(\left(x+y\right)\left(y-x\right)=y^2-x^2\)

3) \(\left(x-y\right)\left(-x-y\right)=-\left(x+y\right)\left(x-y\right)=-\left(x^2-y^2\right)=y^2-x^2\)

6) \(\left(2+3x^2\right)\left(3x^2-2\right)=9x^4-4\)

7) \(\left(\dfrac{1}{2}+x\right)\left(-x+\dfrac{1}{2}\right)=\left(\dfrac{1}{2}+x\right)\left(\dfrac{1}{2}-x\right)=\dfrac{1}{4}-x^2\)

8) \(\left(4m-5n\right)\left(5n+4m\right)=\left(4m-5n\right)\left(4m+5n\right)=16m^2-25n^2\)

9) \(\left(7a+1\right)\left(1-7a\right)=\left(1+7a\right)\left(1-7a\right)=1-49a^2\)

10) \(\left(1+9\right)\left(1-9\right)=1-9^2\)

1.x²-y²+2x+1=(x²+2x+1)-y²=(x+1)²-y²=(x+1-y)(x+1+y)

2.(x²+9)²-36x²=(x²+9)²-(6x)²=(x²+9-6x)(x²+9+6x)=(x-3)²(x+3)²

3.\(8x^3+\dfrac{1}{27}=\left(2x\right)^3+\left(\dfrac{1}{3}\right)^3\\ =\left(2x+\dfrac{1}{3}\right)\text{[}\left(2x\right)^2-2x.\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\text{]}\\ =\left(2x+\dfrac{1}{3}\right)\left(4x^2-\dfrac{2}{3}x+\dfrac{1}{9}\right)\)4.x³-8y³=x³-(2y)³=(x-2y)(x²+2xy+4y²)

a-b=7

(a-b)²=a²+b²-2ab=49

a²+b²+4ab-2ab=49+32=81

(a+b)²=81

a+b=9  hoặc a+b=(-9)

1) \(B=\dfrac{1}{8}x^3-\dfrac{3}{4}x^2+\dfrac{3}{2}x-1=\left(\dfrac{1}{2}x-1\right)^3\)

thay x =-2 vào B, ta được:

\(B=\left(\dfrac{1}{2}\cdot\left(-2\right)-1\right)^3=\left(-2\right)^3=-8\)

2) \(C=x^3+3x^2+3x-999=\left(x+1\right)^3-1000\)

thay x =99 vào B, ta được:

\(C=\left(99+1\right)^3-1000=999000\)

3) \(D=27x^3+54x^2+36x+4=\left(3x+2\right)^3-4\)

thay x =-2 vào D, ta được:

\(D=\left(3\left(-2\right)+2\right)^3-4=-68\)

a: \(F=a^3-b^3-3ab\)

\(=\left(a-b\right)^3+3ab\left(a-b\right)-3ab\)

\(=1^3+3ab-3ab=1\)

b: \(G=a^3-b^3+3ab\)

\(=\left(a-b\right)^3+3ba\left(a-b\right)+3ab\)

=-1

c: \(H=\left(x-1\right)^3\)

(x+1)³=8

=>x+1=2

=>x=1

\(H=\left(1-1\right)^3=0\)

Triển khai hình lập phương không có nắp ta được một hình chữ thập gồm hai hình chữ nhật có chiều rộng 1 (đơn vị dài) và chiều dài 3 (đơn vị dài.).

Sắp xếp như hình vẽ, ta có tam giác vuông cân ở góc nhỏ có cạnh huyền 1 đơn vị dài thì cạnh góc vuông là 2 2 đơn vị dài.

Tam giác vuông cân có cạnh huyền là 3 đơn vị dài thì cạnh góc vuông bằng 3 đơn vị dài.