
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



12 + 14 + 16 + x chia hết cho 2
12 ; 14 ; 16 chia hết cho 2 => x chia hết cho 2
12 + 14 + 16 không chia hết cho 2
12 ; 14 ; 16 chia hết cho 2 => x không chia hết cho 2 (lẻ)

Câu trả lời hay nhất: + ta chứng minh a,b,c có ít nhất một số chia hết cho 3
giả sử cả 3 số trên đều không chia hết cho 3
=> a^2 = 1 (mod3) và b^2 = 1 (mod3) (bình phương 1 số chia hết cho 3 hoạc chia 3 dư 1)
=> a^2 + b^2 = 2 (mod3) nhưng c^2 = 1 (mod3) => mâu thuẫn
Vậy có ít nhất 1 số chia hết cho 3
+ tương tự,có ít nhất 1 số chia hết cho 4,vì giả sử cả 3 số a,b,c đều không chia hết cho 4
=> a^2 = 1 (mod4) và b^2 = 1 (mod4) => a^2 + b^2 = 2 (mod 4) nhưng c^2 = 1 (mod 4) => mâu thuẫn
vậy có ít nhất 1 số cgia hết cho 4
+ tương tự a^2 = 1 (mod 5) hoạc a^2 = -1 (mod 5) hoạc a^2 = 4 (mod 5)
và -1 + 1 = 0,1 + 4 = 5,-1 + 4 = 3
=> phải có ít nhất 1 số chia hết cho 5
Vậy abc chia hết cho BCNN(3,4,5) = 60 hay abc chia hết 60
a+5b ⋮ 7
=> 3(a+5b) ⋮7
=> 3a+15b⋮7
=> 3a+15b +7a -14b⋮7
=> 10a+b⋮7
chúc bn hok tốt ^_^

a,A = 1 + 2 + 22 + 23 +.... + 22013 + 22014
2A = 2 + 22 + 23 + ...... + 22013 + 22014 + 22015
A = ( 2 + 22 + 23 + ..... + 22013 + 22014 + 22015 ) - ( 1 + 2 + 22 + 23 + ..... + 22013 + 22014 )
A = 22015 - 1
b, A = 1 + 2 + 22 + 23 + ... + 22013 + 22014
= ( 1 + 2 + 22 + 23 + 24 ) + .... + ( 22010 + 22011 + 22012 + 22013 + 22014 )
= 31 + ..... + 22010.( 1 + 2 + 22 + 23 + 24 )
= 31 + ..... + 22010 . 31
= 31.1 + ..... + 22010 . 31
= 31. ( 1 + .... + 22010 ) chia hết cho 31
=> A chia hết cho 31
a) \(A=1+2+2^2+2^3+....+2^{2014}\)
\(\Leftrightarrow\)\(2A=2+2^2+2^3+2^4+...+2^{2015}\)
\(\Leftrightarrow\)\(2A-A=\left(2+2^2+2^3+...+2^{2015}\right)-\left(1+2+2^2+...+2^{2014}\right)\)
\(\Leftrightarrow\)\(A=2^{2015}-1\)
b) \(A=1+2+2^2+2^3+...+2^{2014}\)
\(=\left(1+2+2^2+2^3+2^4\right)+\left(2^5+2^6+2^7+2^8+2^9\right)\)\(+...+\left(2^{2010}+2^{2011}+2^{2012}+2^{2013}+2^{2014}\right)\)
\(=\left(1+2+2^2+2^3+2^4\right)+2^5\left(1+2+2^2+2^3+2^4\right)\)\(+...+2^{2010}\left(1+2+2^2+2^3+2^4\right)\)
\(=\left(1+2+2^2+2^3+2^4\right)\left(1+2^5+...+2^{2010}\right)\)
\(=31\left(1+2^5+...+2^{2010}\right)\) \(⋮31\)

+ a - b chia hết cho 5
Mà 5b chia hết cho 5
=> a - b - 5b chia hết cho 5
=> a - 6b chia hết cho 5
+) a - b chia hết cho 5 => 2a - 2b chia hết cho 5
Mà 5b chia hết cho 5
=> 2a - 2b - 5b chia hết cho 5
=> 2a - 7b chia hết cho 5
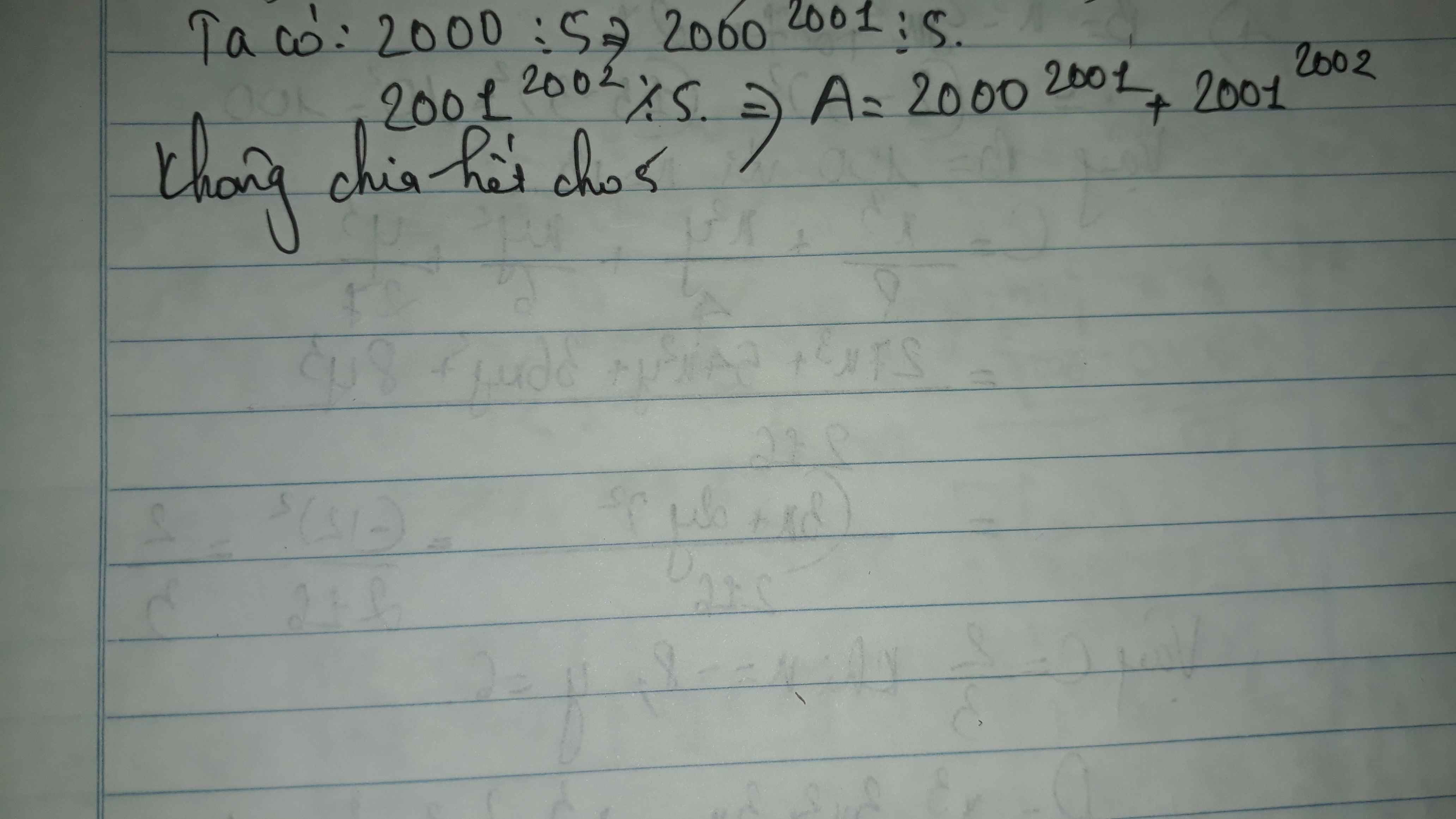
a) 20012002 + 20023
Vì 2001 không chia hết cho 2 => 20012002 không chia hết cho 2
Mà 2002 chia hết cho 2 => 20023 chia hết cho 2
=> 20012002 + 20023 không chia hết cho 2
b) 8617 + 9722
= (...1) + (...4)
= (...5) chia hết cho 5