
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun

3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8

a: Khi m=4 thì (1) sẽ là:
x^2-6x-7=0
=>x=7 hoặc x=-1
b: Sửa đề: 2x1+3x2=-11
x1+x2=2m-2
=>2x1+3x2=-11 và 2x1+2x2=4m-4
=>x2=-11-4m+4=-4m-7 và x1=2m-2+4m+7=6m+5
x1*x2=-2m+1
=>-24m^2-20m-42m-35+2m-1=0
=>-24m^2-60m-34=0
=>\(m=\dfrac{-15\pm\sqrt{21}}{12}\)

Câu 6:
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC

c: Xét ΔHDK vuông tại H và ΔHIB vuông tại H có
góc HDK=góc HIB
=>ΔHDK đồng dạng với ΔHIB
=>HD/HI=HK/HB
=>HD*HB=HI*HK=AH^2

a: \(\Leftrightarrow\left\{{}\begin{matrix}6x+3y=3\\6x+8y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1\end{matrix}\right.\)

2:
A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-3x1x2
=(1/2)^2-3*(-1/4)=1/4+3/4=1

b: \(B=\sqrt{\left(2\sqrt{5}-5\right)^2}+\sqrt{29-12\sqrt{5}}\)
\(=\sqrt{\left(5-2\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{5}-3\right)^2}\)
\(=\left|5-2\sqrt{5}\right|+\left|2\sqrt{5}-3\right|\)
\(=5-2\sqrt{5}+2\sqrt{5}-3=2\)
c: \(C=\dfrac{6}{\sqrt{7}-1}-14\sqrt{\dfrac{1}{7}}+\dfrac{\sqrt{21}+2\sqrt{7}}{2+\sqrt{3}}\)
\(=\dfrac{6\left(\sqrt{7}+1\right)}{7-1}-2\sqrt{7}+\dfrac{\sqrt{7}\left(2+\sqrt{3}\right)}{2+\sqrt{3}}\)
\(=\sqrt{7}+1-2\sqrt{7}+\sqrt{7}=1\)





 cứu tui câu C vớiiii
cứu tui câu C vớiiii

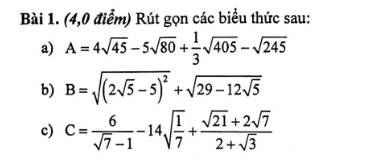
bài 1:
a: \(\left\{{}\begin{matrix}3x+2y=5\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x+2y=5\\4x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=1\\2x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=2-2x=2-2\cdot\left(-1\right)=4\end{matrix}\right.\)
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=5\\x_1x_2=\dfrac{c}{a}=2\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=5^2-2\cdot2=25-4=21\)