Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta xét tỉ số ![]()
Để trên CD có nhiều cực đại thì ![]() nhỏ nhất
nhỏ nhất
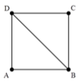
![]() BD có 15 cực đại→ để
BD có 15 cực đại→ để ![]() nhỏ nhất thì tại A và B nằm tại vị trí cách cực đại gần nhất với nó một đoạn gần bằng
nhỏ nhất thì tại A và B nằm tại vị trí cách cực đại gần nhất với nó một đoạn gần bằng ![]() (bằng
(bằng ![]() ứng với A và B là các cực đại)
ứng với A và B là các cực đại) ![]()
+ Thay vào biểu thức trên, ta tìm được
![]()
![]() Trên CD có tối đa 7 cực đại
Trên CD có tối đa 7 cực đại

- Số cực đại trên CD thõa mãn điều kiện:
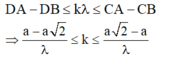
- Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại k = 0 nên: -2 < k < 2
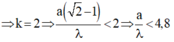
- Số cực đại trên AB:
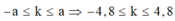
⇒ Số cực đại là 9.

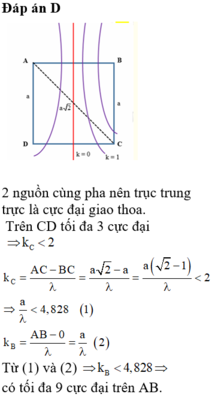
Đáp án D
Số cực đại trên CD thõa mãn điều kiện : D A - D B ≤ k λ ≤ C A - C B
⇒ a - a 2 λ ≤ k ≤ a 2 - a λ
Vì trên CD có 3 cực đại và các cực đại đối xứng qua cực đại k = 0 nên : -2 < k < 2
⇒ k = 2 ⇒ a ( 2 - 1 ) λ < 2 ⇒ a λ < 4 , 8
Số cực đại trên AB - a ≤ k ≤ a ⇒ - 4 , 8 ≤ k ≤ 4 , 8
Số cực đại là 9.

Đáp án B
Lời giải chi tiết:
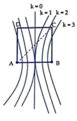
Từ hình vẽ ta thấy để CD có 3 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3.
![]()
![]()
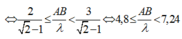
Gọi 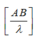 là phần nguyên của tỉ số
A
B
λ
là phần nguyên của tỉ số
A
B
λ
Số điểm dao động với biên độ cực đại trên AB là
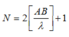
Mà Nmax khi 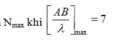
Suy ra, số điểm cực đại trên AB nhiều nhất là 2.7+1=15 điểm.

Đáp án C
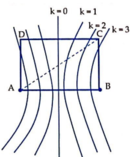
Từ hình vẽ ta thấy để trên CD có 5 điểm dao động với biên độ cực đại thì điểm C phải nằm giữa đường cực đại bậc 2 và đường cực đại bậc 3.
![]()
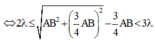
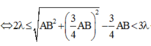
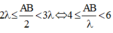
 giá trị lớn nhất là 5.
giá trị lớn nhất là 5.
Suy ra, số cực đại tối đa trên AB là 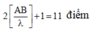


Đáp án B.
Trên AB có 15 vị trí dao động với biên độ cực đại do vậy ta có AB < 8λ
Xét M thuộc trên CD ta có
Vậy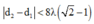
Mặt khác M là cực đại giao thoa thì:
Do đó ta được
Vậy có 7 giá trị k; tương ứng có tối đa 7 cực đại giao thoa trên CD.