Ta có (40;31) = 1 nên phương trình có nghiệm nguyên

Tìm nghiệm riêng của pt

40 = 31.1 + 9

31 = 9.3 + 4

9 = 4.2 + 1

\(\Rightarrow40.7+31.\left(-9\right)=1\)

\(\Rightarrow\hept{\begin{cases}x_0=7\\y_0=-9\end{cases}}\)

Vậy phương trình có nghiệm nguyên là \(\hept{\begin{cases}x=7+31t\\y=-9-40t\end{cases}\left(t\in Z\right)}\)

\(11x+8y=73\)

\(\Rightarrow11x+8y=33+40\)

\(\Rightarrow11x+8y=11.3+8.5\)

\(\Rightarrow\hept{\begin{cases}x=3\\y=5\end{cases}}\)

âm thì sao bạn

6x²-3xy+17x-4y+5=0

⇔ -3xy-4y=-6x²-17x-5

⇔ 3xy+4y=6x²+17x+5

⇔ y(3x+4)=6x²+17x+5

6x²+17x+5 ⋮ 3x-4 vì x, y ∈ Z

⇔ 6x²+17x+12-7 ⋮ 3x+4

⇔ 6x²+8x+9x+12-7 ⋮ 3x+4

⇔ 2x(3x+4)+3(3x+4)-7 ⋮ 3x+4

=> 7 ⋮ 3x+4

=> 3x+4 ∈ Ư(7)={-1,1,-7,7}

3x+4=1 ⇔ x=-1 (lấy)

3x+4=-1 ⇔ x=\(\dfrac{-5}{3}\) (loại)

3x+4=-7 ⇔ x=\(\dfrac{-11}{3}\)(loại)

3x+4=7 ⇔ x=1 (lấy)

thay vào tính thì y={-6,4} (bạn tự làm nhá)

vậy (x,y)={(-1,1),(-6,4)}

Ta có: \(7\left(x^2+xy+y^2\right)=39\left(x+y\right)\)  nên \(x^2+xy+y^2⋮39\)   \(x+y⋮7\)

 Đặt \(x^2+xy+y^2=39k;x+y=7k\)  \(\left(k\in N\right)\)   vì  \(x^2+xy+y^2\ge0\)

  \(\Rightarrow xy=\left(x+y\right)^2-\left(x^2+xy+y^2\right)=49k^2-39k\)

Theo Viet x,y là nghiệm của phương trình \(a^2-49k^2a+49k^2-39k=0\)

  Phương trình có 2 nghiệm khi \(\Delta=49k^2-4.49k^2+4.39k=156k-147k^2=k\left(156-147k\right)\ge0\)

  Vì k>0 nên \(156>147k\), vì k nguyên nên k=1

Do đó ta có x + y = 7,xy=10 nên áp dụng viet, ta giải được (x,y)=(2;5);(5;2)

Đó là giá trị nguyên cần tìm

Phương trình bậc hai y2 – 8y + 16 = 0

Có a = 1; b = -8; c = 16; Δ = b2 – 4ac = (-8)2 – 4.1.16 = 0.

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :

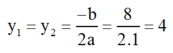
Vậy phương trình có nghiệm kép y = 4.

Với câu a)bạn nhân cả 2 vế cho 12 rồi ép vào dạng bình phương 3 số

Câu b)bạn nhân cho 8 mỗi vế rồi ép vào bình phương 3 số 

giải zõ hộ

a.

\(\Leftrightarrow8x^3+8x=8y^2\)

\(\Leftrightarrow x\left(x^2+1\right)=y^2\)

Gọi \(d=ƯC\left(x;x^2+1\right)\)

\(\Rightarrow x^2+1-x.x⋮d\)

\(\Rightarrow1⋮d\)

\(\Rightarrow x\) và \(x^2+1\) nguyên tố cùng nhau

\(\Rightarrow\left\{{}\begin{matrix}x=m^2\\x^2+1=n^2\end{matrix}\right.\)

\(x^2+1=n^2\Rightarrow\left(n-x\right)\left(n+x\right)=1\)

\(\Rightarrow x=0\)

\(\Rightarrow y=0\)

TH1: a;b;c đồng dư khi chia 3 \(\Rightarrow a+b+c⋮3\)

TH2: 3 số a;b;c có số dư đôi một khác nhau khi chia cho 3 \(\Rightarrow a+b+c⋮3\)

TH3: 3 số a;b;c có 2 số đồng dư khi chia 3, một số khác số dư. Không mất tính tổng quát, giả sử \(a,b\) đồng dư khi chia 3 còn c khác số dư

\(\Rightarrow\left(a-b\right)^2⋮3\) còn \(\left(a-c\right)^2+\left(b-c\right)^2\) chia 3 luôn dư 1 hoặc 2

\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2⋮̸3\)  (1)

Mặt khác từ giả thiết:

\(\left\{{}\begin{matrix}b^2-ac+3ac⋮3\\c^2-ab-3ab⋮3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b^2-ac⋮3\\c^2-ab⋮3\end{matrix}\right.\)

\(\Rightarrow2\left(a^2-bc\right)+2\left(b^2-ac\right)+2\left(c^2-ab\right)⋮3\)

\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2⋮3\) trái với (1) ktm

Vậy \(a+b+c⋮3\)