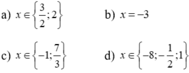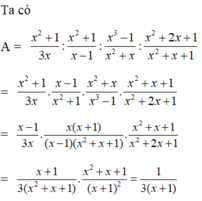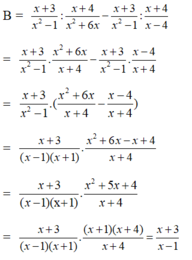Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
= 0 - 0
= 0
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2)
= (x-xx+1) : (2x-2) : (x-xx+1) : (2x-2)
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
= -2x-1-xx2+1. (14 - 4x)
= -x2-1-xx2+14-4x
= -6x-xx2+13

a) Tìm được x = 2,2
b) Tìm được x = 2073
c) Tìm được x = 4 hoặc x = -2
d) Điều kiện x≠-1 . Tìm được x = 0 hoặc x = 3

a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
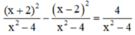
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
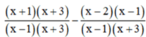
![]()
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)