
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(AB\perp\left(BCD\right)\Rightarrow BD\) là hình chiếu vuông góc của AD lên (BCD)
\(\Rightarrow\widehat{ADB}\) là góc giữa AD và (BCD)
\(tan\widehat{ADB}=\dfrac{AB}{BD}=\sqrt{3}\Rightarrow\widehat{ADB}=60^0\)

35.
\(y'=5cos^4\left(2-3x\right).\left[cos\left(2-3x\right)\right]'\)
\(=5cos^4x.\left(-sin\left(2-3x\right)\right).\left(2-3x\right)'\)
\(=15cos^4\left(2-3x\right).sin\left(2-3x\right)\)
\(\Rightarrow\left\{{}\begin{matrix}m=15\\n=4\end{matrix}\right.\) \(\Rightarrow m+n=19\)
36.
\(U_2=2-\dfrac{1}{2}=\dfrac{3}{2}\) ; \(u_3=2-\dfrac{1}{\dfrac{3}{2}}=\dfrac{4}{3}\) ; \(u_5=2-\dfrac{1}{\dfrac{4}{3}}=\dfrac{5}{4}\)
\(\Rightarrow\) Quy nạp được \(u_n=\dfrac{n+1}{n}\)
\(\Rightarrow\lim\left(u_n\right)=\lim\dfrac{n+1}{n}=1\)
37.
\(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{x^2+7}-4}{2x-6}=\lim\limits_{x\rightarrow3}\dfrac{x^2-9}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{2\left(x-3\right)\left(\sqrt{x^2+7}+4\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x+3}{2\left(\sqrt{x^2+7}+4\right)}=\dfrac{6}{2\left(\sqrt{9+7}+4\right)}=\dfrac{3}{8}\)
Hàm liên tục trên R khi:
\(\dfrac{3}{8}=1-2m\Rightarrow m=\dfrac{5}{16}\in\left(0;1\right)\)

\(a=\lim\limits_{x\rightarrow-3}\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}=\lim\limits_{x\rightarrow-3}\dfrac{1}{x-3}=-\dfrac{1}{6}\)
\(b=\lim\limits_{x\rightarrow2}\dfrac{\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+3}{x+2}=\dfrac{5}{4}\)
\(c=\lim\limits_{x\rightarrow4}\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x+5\right)\left(x-4\right)}=\lim\limits_{x\rightarrow4}\dfrac{x+4}{x+5}=\dfrac{8}{9}\)
\(d=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+2}{x-1}=4\)
\(e=\lim\limits_{x\rightarrow2}\dfrac{x+7-9}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x-2}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{1}{\sqrt{x+7}+3}=\dfrac{1}{6}\)
\(f=\lim\limits_{x\rightarrow1}\dfrac{x+3-4}{\left(x-1\right)\left(\sqrt{x+3}+2\right)}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(\sqrt{x+3}+2\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{\sqrt{x+3}+2}=\dfrac{1}{4}\)
\(h=\lim\limits_{x\rightarrow-3}\dfrac{x+7-4}{\left(x+3\right)\left(\sqrt{x+7}+2\right)}=\lim\limits_{x\rightarrow-3}\dfrac{x+3}{\left(x+3\right)\left(\sqrt{x+7}+2\right)}=\lim\limits_{x\rightarrow-3}\dfrac{1}{\sqrt{x+7}+2}=\dfrac{1}{4}\)
Bài 1:
a,
= limx->-3 \(\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}\)
= limx->3 x-3
= -3 -3
= -6
b,
= limx->2 \(\dfrac{\left(x-2\right)\left(x+3\right)}{\left(x-2\right)\left(x+2\right)}\)
= limx->2 \(\dfrac{x+3}{x+2}\)
= \(\dfrac{5}{4}\)
c,
= limx->4 \(\dfrac{\left(x-4\right)\left(x+4\right)}{\left(x-4\right)\left(x+5\right)}\)
= limx->4 \(\dfrac{\left(x+4\right)}{\left(x+5\right)}\)
= \(\dfrac{8}{9}\)
d,
= limx->2 \(\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x-1\right)}\)
= limx->2 \(\dfrac{\left(x+2\right)}{\left(x-1\right)}\)
= 4

a.
\(y'=\left(x^2\right)'-\left(cosx\right)'=2x-\left(-sinx\right)=2x+sinx\)
b.
\(y'=\left(3sinx\right)'+\left(2cosx\right)'=3cosx+\left(-2sinx\right)=3cosx-2sinx\)
c.
\(y'=\left(5cos\left(2x-\dfrac{\pi}{4}\right)\right)'=5\left(2x-\dfrac{\pi}{4}\right)'.\left(-sin\left(2x-\dfrac{\pi}{4}\right)\right)=-10sin\left(2x-\dfrac{\pi}{4}\right)\)

Bài 2:
Khai triển tử số và mẫu số ta có:
\(\frac{x^4-10x^3+35x^2-50x+24}{256x^4-256x^3+96x^2-16x+1}\)
Nhân cả tử và mẫu với \(\frac{1}{x^4}\) ta có:
\(\frac{1-\frac{10}{x}+\frac{35}{x^2}-\frac{50}{x^3}+\frac{24}{x^4}}{256-\frac{256}{x}+\frac{96}{x^2}-\frac{16}{x^3}+\frac{1}{x^4}}\)
Vậy ta tính dc giới hạn là \(\frac{1}{256}\)
Bài 3:
Ta có: \(\left\{\begin{matrix}\left(2x-3\right)^{20}\in O\left(x^{20}\right)\\\left(3x-3\right)^{20}\in O\left(x^{20}\right)\\\left(2x+1\right)^{30}\in O\left(x^{30}\right)\end{matrix}\right.\). Khi đó giới hạn
\(\lim\limits_{x\rightarrow+\infty}\frac{\left(2x-3\right)^{20}\left(3x-3\right)^{20}}{\left(2x+1\right)^{50}}\) tương đương với
\(\lim\limits_{x\rightarrow+\infty}\ \frac{x^{40}}{x^{50}}=\lim\limits_{x\rightarrow+\infty}\ \frac{1}{x^{10}}=0\)
Bài 1: \(\lim\limits_{x\rightarrow0}\frac{\sqrt[3]{1+x^2}-1}{x^2}\)
Bài 2: \(\lim\limits_{x\rightarrow+\infty}\frac{\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)}{\left(4x-1\right)^4}\)
Bài 3:\(\lim\limits_{x\rightarrow+\infty}\frac{\left(2x-3\right)^{20}\left(3x-3\right)^{20}}{\left(2x+1\right)^{50}}\)
P/s: hoc24 hạn chế đăng câu hỏi bằng hình ảnh nhé, còn n~ t/h gấp thì bn lên đăng thẳng 1 tí

\(\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x+2\cos^2x-1\right)-\sin2x-\cos x=0\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x+2\cos^2x-1-2\cos^2x+1-\cos x\right)=0\Leftrightarrow\left(2\sin x+1\right)\left(\sqrt{3}\sin x-\cos x\right)=0\Rightarrow\left[{}\begin{matrix}2\sin x+1=0\\\sqrt{3}\sin x-\cos x=0\end{matrix}\right.\)







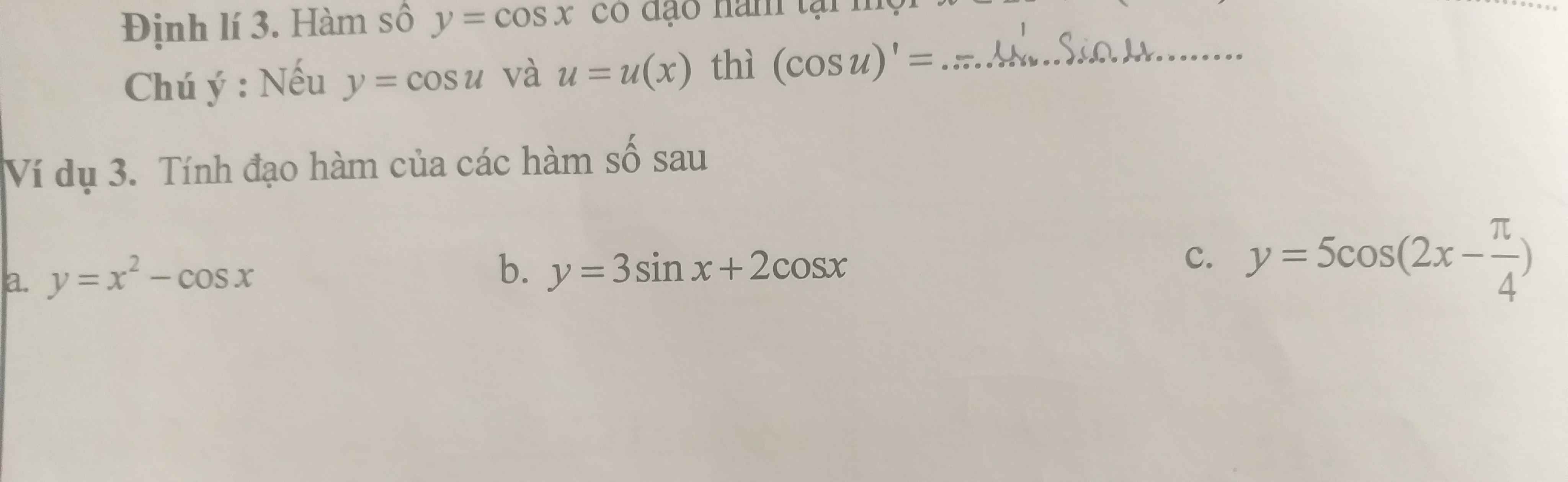

1. \(y'=6x^2+6x\Rightarrow y'\left(1\right)=12\)
Đáp án B
2. \(y'=\dfrac{7}{\left(x+3\right)^2}\Rightarrow y'\left(1\right)=\dfrac{7}{16}\) (A)
3. \(y'=8x^3+9x^2-3\Rightarrow y'\left(3\right)=294\)
Tất cả các đáp án đều sai
4. Tiếp tục là 1 câu đề bài sai
Hàm số không xác định tại \(x=1\Rightarrow\) không liên tục tại \(x=1\Rightarrow\) không tồn tại đạo hàm tại \(x=1\)
5.
\(f'\left(x\right)=7x^6+20x^4+6x\)
\(\Rightarrow f'\left(2\right)=780\)
6.
\(y'=\dfrac{3}{\left(x+1\right)^2}\)
\(\Rightarrow y'\left(2\right)=\dfrac{1}{3}\) ; \(y\left(2\right)=1\)
Phương trình tiếp tuyến:
\(y=\dfrac{1}{3}\left(x-2\right)+1\Leftrightarrow y=\dfrac{1}{3}x+\dfrac{1}{3}\)