
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số người mua là x(người), doanh thu là y(đồng)
(Điều kiện: \(x\in Z^+;y>0\))
Vì doanh thu bằng số người mua nhân với lại giá của bộ quần áo nên y=320000x(đồng)
=>\(320000=\dfrac{y}{x}\)
Số người mua tăng lên 60% và doanh thu cũng tăng thêm 30% nên giá mới sẽ là:
\(\dfrac{y\cdot\left(1+30\%\right)}{x\left(1+60\%\right)}=\dfrac{y}{x}\cdot\dfrac{13}{16}=320000\cdot\dfrac{13}{16}=260000\left(đồng\right)\)

a: ĐKXĐ x>0; x<>1
\(A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{1}=\dfrac{x-1}{\sqrt{x}}\)
b: A<0
=>x-1<0
=>0<x<1

Bạn tự tìm điều kiện xác định nhé :)
\(Q=\left(1-\frac{x-3\sqrt{x}}{x-9}\right):\left(\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}-\frac{9-x}{x+\sqrt{x}-6}\right)\)
\(=\frac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}:\left(\frac{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)+\left(\sqrt{x}-2\right)^2-9+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\)
\(=\frac{3}{\sqrt{x}+3}:\frac{9-x+x-4\sqrt{x}+4-9+x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\frac{3}{\sqrt{x}+3}:\frac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{3}{\sqrt{x}+3}.\frac{\sqrt{x}+3}{\sqrt{x}-2}=\frac{3}{\sqrt{x}-2}\)

Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x^2+x+2=0\\y=-x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-x-2=0\\y=-x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\y=-x-2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(2;-4\right);\left(-1;-1\right)\right\}\)


Lời giải:
\(S_{ABC}=\frac{AE.BC}{2}=\frac{3.\frac{25}{4}}{2}=9,375\) (cm vuông)
Dễ thấy $AIEJ$ là hình chữ nhật, nên:
$S_{AIEJ}=AI.AJ$
Áp dụng hệ thức lượng trong tam giác vuông với tam giác $AEB$ và $AEC$ ta có:
\(AI.AB=AE^2; AJ.AC=AE^2\)
\(\Rightarrow AI.AJ=\frac{AE^4}{AB.AC}=\frac{3^4}{2S_{ABC}}=\frac{3^4}{2.9,375}=4,32\) (cm vuông)

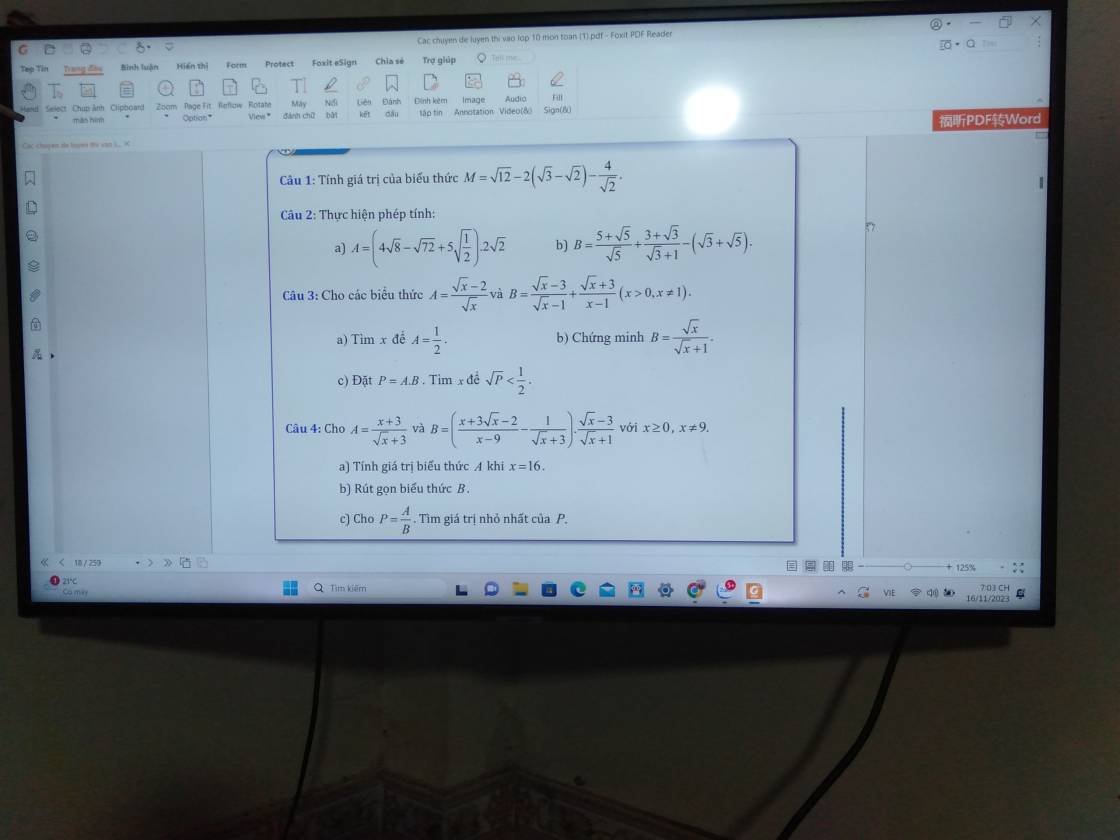
Câu 3:
a: A=1/2
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
=>\(2\sqrt{x}-4=\sqrt{x}\)
=>\(2\sqrt{x}-\sqrt{x}=4\)
=>\(\sqrt{x}=4\)
=>x=16(nhận)
b: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{x-1}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
\(\sqrt{P}< \dfrac{1}{2}\)
=>\(0< =P< \dfrac{1}{4}\)
=>P>=0 và P<1/4
=>P>=0 và P-1/4<0
=>\(\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}+1}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+1}-\dfrac{1}{4}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}-2>=0\\\dfrac{4\sqrt{x}-8-\sqrt{x}-1}{4\left(\sqrt{x}+1\right)}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>=2\\3\sqrt{x}-9< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}>=2\\\sqrt{x}< 3\end{matrix}\right.\)
=>\(2< =\sqrt{x}< 3\)
=>4<=x<9
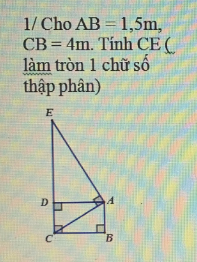 giải giúp mình vớii
giải giúp mình vớii



1)Tco ABCD là hình chữ nhật ( ADC=DCB=ABC=\(90^o\))
=> DC= AB=1,5(m)
=>AD=BC=4(m)
Xét tam giác ACE vuông tại A có đường cao AD
=>\(AD^2=DC.DE\)
\(\Leftrightarrow DE=\dfrac{AD^2}{DC}=\dfrac{16}{1,5}=10,7\)(m)
\(\Leftrightarrow CE=DE+DC=1,5+10,7=12,2\left(m\right)\)