
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)

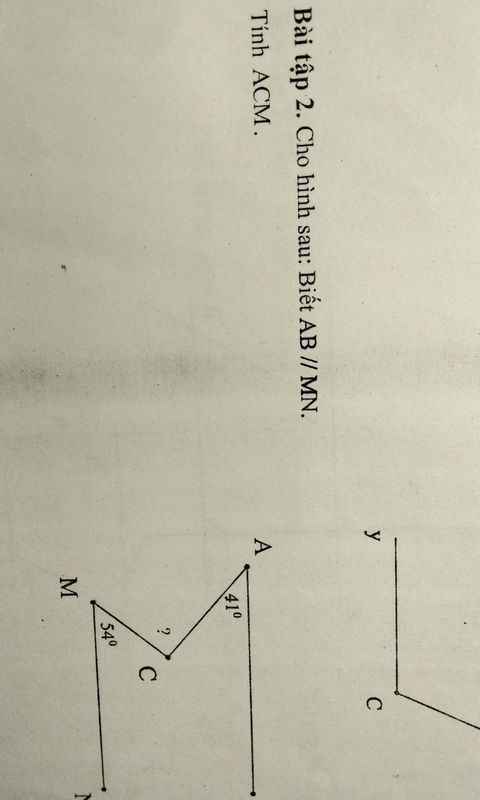
Kẻ CD//AB thì CD//MN
Do đó \(\widehat{ACD}=\widehat{CAB}=41^0;\widehat{MCD}=\widehat{CMN}=54^0\) (so le trong)
Vậy \(\widehat{ACM}=\widehat{ACD}+\widehat{DCM}=41^0+54^0=95^0\)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
b: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc EBF chung
=>ΔBEF=ΔBAC
=>BF=BC
=>ΔBFC cân tại B
c: Xét ΔBFC có BA/BF=BE/BC
nên AE//CF
d: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại D
=>D là trực tâm
=>BD vuông góc FC

a: góc xOt=góc yOt=100/2=50 độ
b: góc xOt'=180 độ-góc xOt=130 độ


1) Ta có: |x+3| \(\ge\)0; |2x+y-4| \(\ge\)0
\(\Rightarrow\) |x + 3| + |2x + y - 4| \(\ge\) 0
Dấu = xảy ra khi x+3=0 và 2x+y-4 = 0 \(\Rightarrow\)x=-3; y=10
1) |x + 3| + |2x + y - 4| = 0
\(\Leftrightarrow\hept{\begin{cases}x+3=0\\2x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\-6+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\y=10\end{cases}}\)

a: Ta có: \(\left|x-0.6\right|< \dfrac{1}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-0.6\ge0\\x-0.6< \dfrac{1}{3}\end{matrix}\right.\Leftrightarrow0.6\le x< \dfrac{14}{15}\)

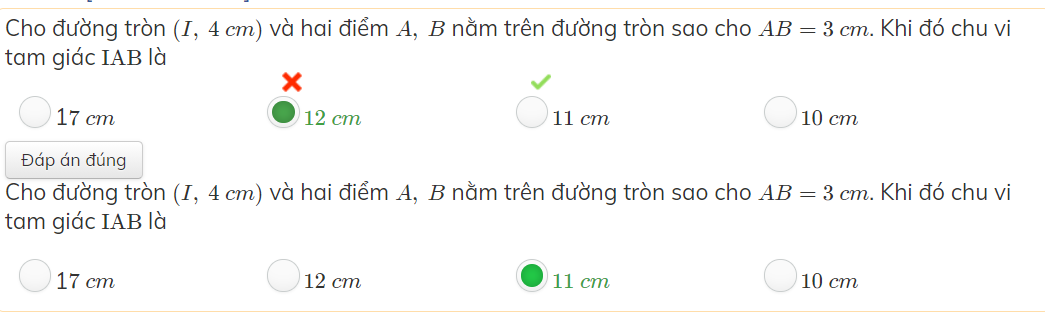
A, B thuộc đường tròn nên \(IA=IB=R=4\left(cm\right)\)
Chu vi tam giác: \(IA+IB+AB=4+4+3=11\left(cm\right)\)
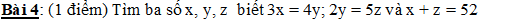



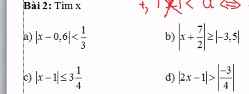
`A(x)=P(x)-Q(x)`
`=-5x+10+6x^3-6x^2+2x-(x^3-5x+5x^3+4-x^2)`
`=6x^3-6x^2-3x+10-(6x^3-x^2-5x+4)`
`=6x^3-6x^3-6x^2+x^2-3x+5x+10-4`
`=-5x^2+2x+6`
Đặt `A(x)=0`
`=>-5x^2+2x+6=0`
`=>5x^2-2x-6=0`
`=>x^2-2/5x-6/5=0`
`=>(x-1/5)^2=31/25`
`=>x=(+-sqrt{31}+1)/5`
8 A
15 D