
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
TXĐ:D=R
\(f\left(-x\right)=2\cdot\left(-x\right)^4-3\cdot\left(-x\right)^2+1\)
\(=2x^4-3x^2+1=f\left(x\right)\)
=>f(x) là hàm số chẵn


a. Gọi \(E\left(x;y\right)\Rightarrow\overrightarrow{EA}=\left(1-x;3-y\right)\) ; \(\overrightarrow{EB}=\left(5-x;4-y\right)\) ; \(\overrightarrow{ED}=\left(-3-x;-4-y\right)\)
\(\Rightarrow\overrightarrow{EA}+\overrightarrow{ED}-3\overrightarrow{EB}=\left(x-17;y-13\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-17=0\\y-13=0\end{matrix}\right.\) \(\Rightarrow E\left(17;13\right)\)
b. Hạ AH vuông góc CD
\(S_{ADI}=\dfrac{1}{2}AH.DI\) ; \(S_{ABCD}=\dfrac{1}{2}AH.\left(AB+CD\right)\)
\(\Rightarrow\dfrac{1}{2}AH.DI=\dfrac{3}{5}.\dfrac{1}{2}AH\left(AB+CD\right)\)
\(\Rightarrow DI=\dfrac{3}{5}\left(AB+CD\right)=\dfrac{3}{5}\left(AB+DI+AB\right)\)
\(\Leftrightarrow\dfrac{2}{5}DI=\dfrac{6}{5}AB\Rightarrow DI=3AB\)
\(\Rightarrow\overrightarrow{DI}=3\overrightarrow{AB}\Rightarrow I\left(9;-1\right)\)
Phương trình AI: \(x+2y-7=0\)
Phương trình BD: \(x-y-1=0\)
Tọa độ M là nghiệm: \(\left\{{}\begin{matrix}x+2y-7=0\\x-y-1=0\end{matrix}\right.\) \(\Rightarrow M\left(3;2\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}5x^2+5y^2+5xy-15=0\\2x^2+2y^2-xy+x+y=5\end{matrix}\right.\)
Trừ vế cho vế của pt trên cho pt dưới:
\(3x^2+3y^2+6xy-\left(x+y\right)-15=-5\)
\(\Leftrightarrow3\left(x+y\right)^2-\left(x+y\right)-10=0\)
\(\Rightarrow\left[{}\begin{matrix}x+y=2\\x+y=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y=2-x\\y=-\dfrac{5}{3}-x\end{matrix}\right.\)
Thay vào pt đầu giải pt bậc 2 một ẩn như bt

2.
a, Theo định lí hàm số sin:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow sinA=\dfrac{b}{a}sinB=\dfrac{c}{a}sinC\)
Khi đó: \(2sinA=sinB+sinC\)
\(\Leftrightarrow2sinA=\dfrac{b}{a}sinA+\dfrac{c}{a}sinA\)
\(\Leftrightarrow2=\dfrac{b}{a}+\dfrac{c}{a}\)
\(\Leftrightarrow b+c=2a\) đúng theo giả thiết
\(\Rightarrowđpcm\)
b, Ta có \(S_{ABC}=\dfrac{1}{2}a.h_a=\dfrac{1}{2}b.h_b=\dfrac{1}{2}c.h_c\)
\(\Rightarrow\left\{{}\begin{matrix}h_a=\dfrac{2.S_{ABC}}{a}\\h_b=\dfrac{2.S_{ABC}}{b}\\h_c=\dfrac{2.S_{ABC}}{c}\end{matrix}\right.\)
Khi đó: \(\dfrac{2}{h_a}=\dfrac{1}{h_b}+\dfrac{1}{h_c}\)
\(\Leftrightarrow\dfrac{2}{\dfrac{2.S_{ABC}}{a}}=\dfrac{1}{\dfrac{2.S_{ABC}}{b}}+\dfrac{1}{\dfrac{2.S_{ABC}}{c}}\)
\(\Leftrightarrow\dfrac{a}{S_{ABC}}=\dfrac{b}{2.S_{ABC}}+\dfrac{c}{2.S_{ABC}}\)
\(\Leftrightarrow b+c=2a\) đúng theo giả thiết
\(\Rightarrowđpcm\)


5:
a: (C): x^2-4x+4+y^2-2y+1-9=0
=>(x-2)^2+(y-1)^2=9
=>R=3; I(2;1)
b: vecto IM=(-1;3)
=>(d) có VTPT là (-1;3)
Phương trình d là;
-1(x-1)+3(y-4)=0
=>-x+1+3y-12=0
=>-x+3y-11=0

Pt đã cho có nghiệm duy nhất khi và chỉ khi:
\(m^2-4\ne0\Rightarrow m\ne\pm2\)
\(\Rightarrow\) Có \(5-\left(-5\right)+1-2=9\) giá trị nguyên của m



 Giải hộ với ạ
Giải hộ với ạ  hộ em với
hộ em với 
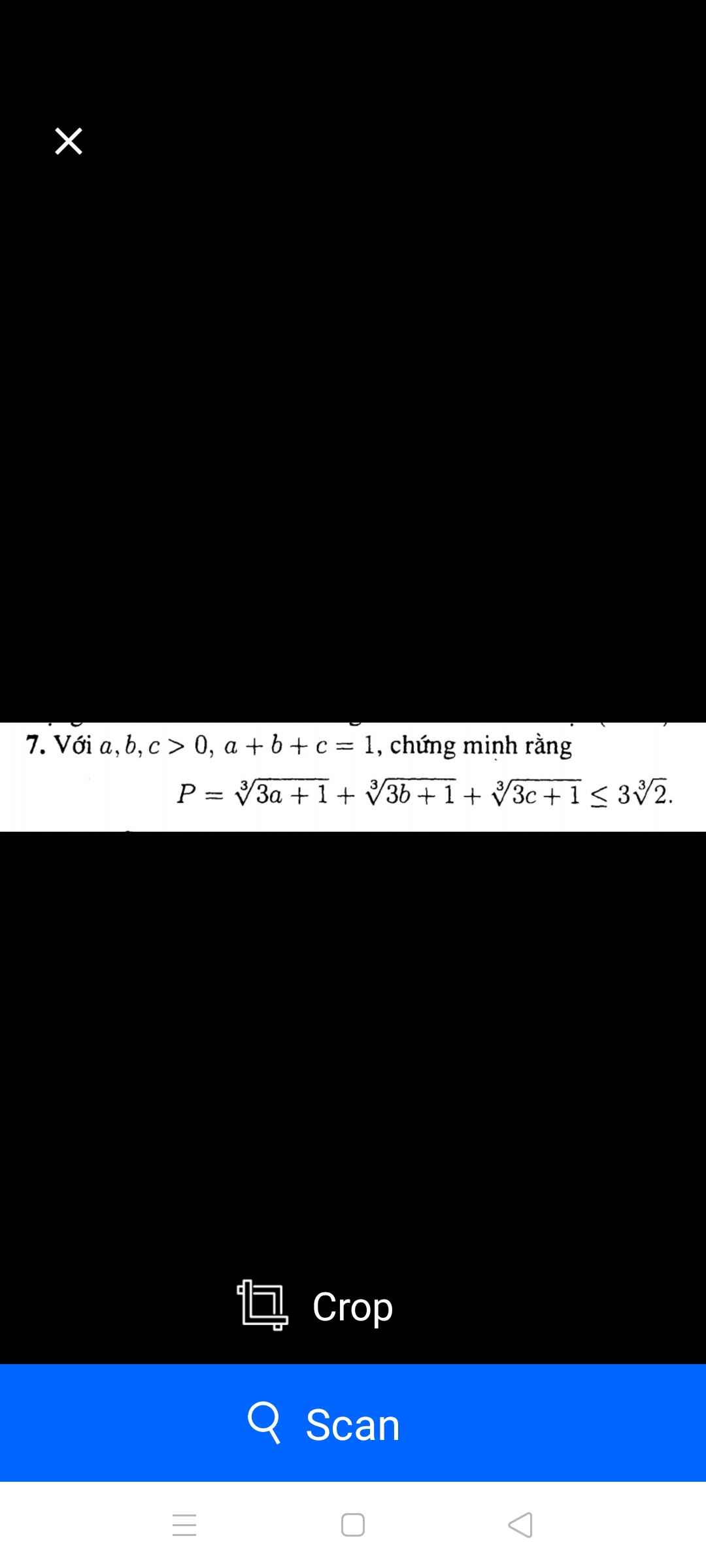



 iải chi tiết hộ em với
iải chi tiết hộ em với
tự đi mà giải nha tui phá kênh rồi