K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 6 2019
2.lxl-12x-x=-3-9
2.lxl-13x=-12
2x-13x=-12;x>=0
2.(-x)-13x=-12;x<0
x=12/11;x>=0
x=4/5;x<0
DT
2
KN
9 tháng 6 2019
a)\(ĐKXĐ:x\ge\frac{-1}{2}\)
\(\sqrt{x^2+4x+4}=2x+1\)
\(\Leftrightarrow\sqrt{\left(x+2\right)^2}=2x+1\)
\(\Leftrightarrow x+2=2x+1\)
\(\Leftrightarrow-x=-1\)
\(\Leftrightarrow x=1\)
Vậy nghiệm duy nhất của phương trình là 1.
KN
9 tháng 6 2019
b)\(ĐKXĐ:x\ge3\)
\(\sqrt{4x^2-12x+9}=x-3\)
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=x-3\)
\(\Leftrightarrow2x-3=x-3\)
\(\Leftrightarrow2x=x\)
\(\Leftrightarrow x=0\)(không t/m đkxđ)
Vậy phương trình vô nghiệm
HN
1
16 tháng 9 2023
a: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(x-3\right)^2}=3-x\)
=>|x-3|=3-x
=>x-3<=0
=>x<=3
b:
ĐKXĐ: x thuộc R
\(\sqrt{4x^2-20x+25}+2x=5\)
=>|2x-5|=5-2x
=>2x-5<=0
=>x<=5/2
c: ĐKXĐ: \(x\in R\)
PT =>căn (6x-1)^2=5
=>|6x-1|=5
=>6x-1=5 hoặc 6x-1=-5
=>6x=-4 hoặc 6x=6
=>x=1 hoặc x=-2/3
25 tháng 8 2023
a) \(\sqrt[]{x^2-4x+4}=x+3\)
\(\Leftrightarrow\sqrt[]{\left(x-2\right)^2}=x+3\)
\(\Leftrightarrow\left|x-2\right|=x+3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=x+3\\x-2=-\left(x+3\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0x=5\left(loại\right)\\x-2=-x-3\end{matrix}\right.\)
\(\Leftrightarrow2x=-1\Leftrightarrow x=-\dfrac{1}{2}\)
b) \(2x^2-\sqrt[]{9x^2-6x+1}=5\)
\(\Leftrightarrow2x^2-\sqrt[]{\left(3x-1\right)^2}=5\)
\(\Leftrightarrow2x^2-\left|3x-1\right|=5\)
\(\Leftrightarrow\left|3x-1\right|=2x^2-5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=2x^2-5\\3x-1=-2x^2+5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x^2-3x-4=0\left(1\right)\\2x^2+3x-6=0\left(2\right)\end{matrix}\right.\)
Giải pt (1)
\(\Delta=9+32=41>0\)
Pt \(\left(1\right)\) \(\Leftrightarrow x=\dfrac{3\pm\sqrt[]{41}}{4}\)
Giải pt (2)
\(\Delta=9+48=57>0\)
Pt \(\left(2\right)\) \(\Leftrightarrow x=\dfrac{-3\pm\sqrt[]{57}}{4}\)
Vậy nghiệm pt là \(\left[{}\begin{matrix}x=\dfrac{3\pm\sqrt[]{41}}{4}\\x=\dfrac{-3\pm\sqrt[]{57}}{4}\end{matrix}\right.\)
TT
1
16 tháng 7 2021
Ta có: \(\sqrt{9x+9}+\sqrt{4x+4}-2\sqrt{16x+16}=\sqrt{x+1}-8\)
\(\Leftrightarrow3\sqrt{x+1}+2\sqrt{x+1}-8\sqrt{x+1}-\sqrt{x+1}=-8\)
\(\Leftrightarrow\sqrt{x+1}=2\)
\(\Leftrightarrow x+1=4\)
hay x=3
NH
1
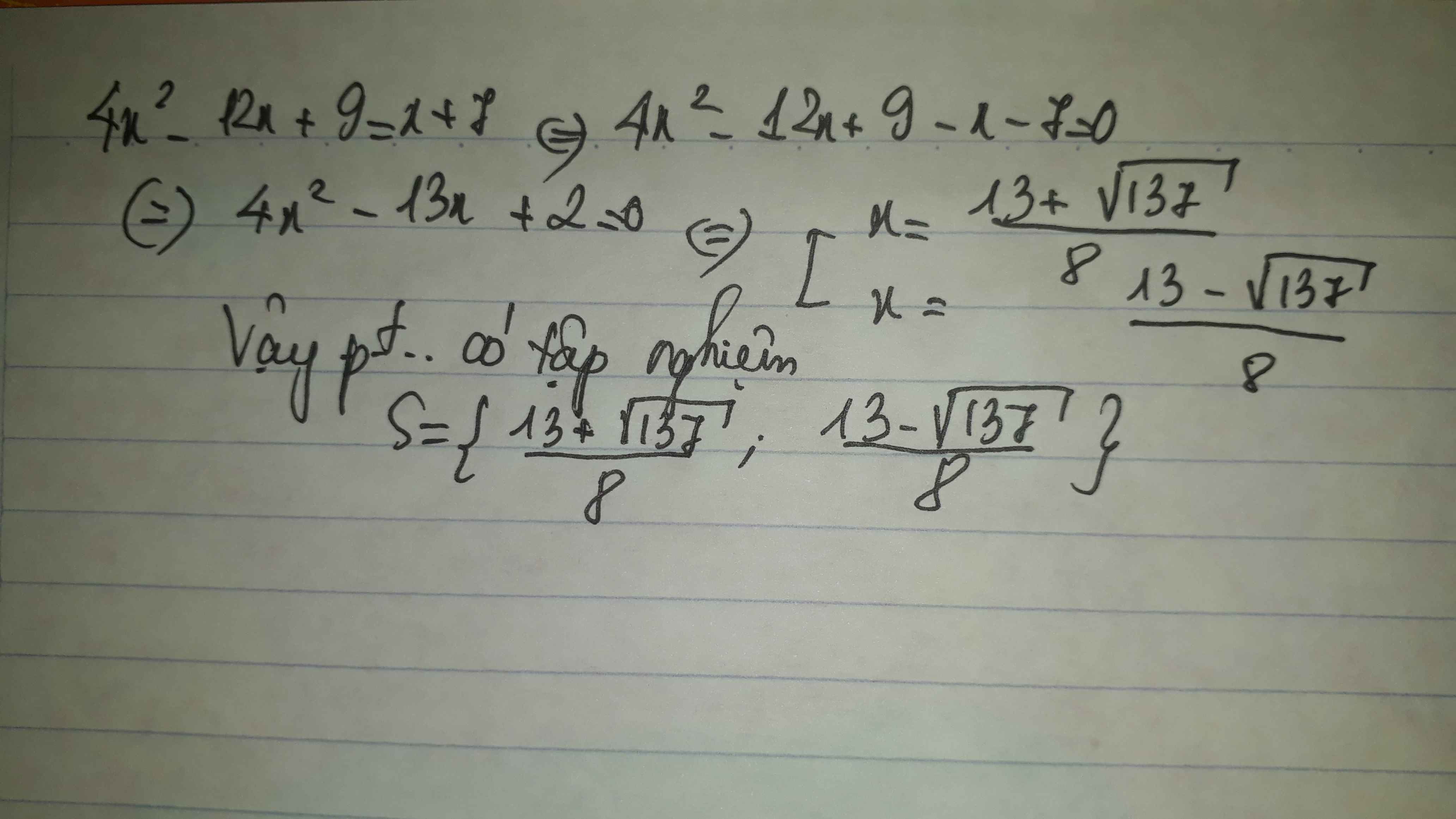
\(\sqrt{4x^2-12x+9}=x-3\)
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=x-3\)
\(\Leftrightarrow|2x-3|=x-3\)
Xét 2 trường hợp :
TH1 : Nếu \(2x-3>0\Rightarrow x>\frac{3}{2}\)thì \(|2x-3|=2x-3\).Khi đó ta có PT:
\(2x-3=x-3\)
\(\Leftrightarrow2x-x=-3+3\)
\(\Leftrightarrow x=0\)( loại vì \(x>\frac{3}{2}\))
TH2: Nếu \(2x-3< 0\Rightarrow x< \frac{3}{2}\)thì \(|2x-3|=3-2x\).Khi đó ta có PT:
\(3-2x=x-3\)
\(\Leftrightarrow-2x-x=-3-3\)
\(\Leftrightarrow-3x=-6\)
\(\Leftrightarrow x=2\)( loại vì \(x< \frac{3}{2}\))
Vậy PT vô nghiệm
\(ĐKXĐ:x\ge3\)
\(\sqrt{4x^2-12x+9}=x-3\)
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=x-3\)
Mà \(x\ge3\) nên \(2x-3\ge3\)
\(\Rightarrow\sqrt{\left(2x-3\right)^2}=2x-3\)
\(\Rightarrow2x-3=x-3\)
\(\Leftrightarrow x=0\)(không t/m đkxđ)
Vậy tập nghiệm của phương trình \(S=\left\{\varnothing\right\}\)
P/S: KO CHẮC