Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f) Ta có: \(\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\)
\(\Leftrightarrow4\left|x+1\right|-3\left|x+1\right|=4\)
\(\Leftrightarrow\left|x+1\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=4\\x+1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
g) Ta có: \(\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\)
\(\Leftrightarrow5\sqrt{x+1}-\sqrt{x+1}=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1

Câu 1 là \(\left(8x-4\right)\sqrt{x}-1\) hay là \(\left(8x-4\right)\sqrt{x-1}\)?
Câu 1:ĐK \(x\ge\frac{1}{2}\)
\(4x^2+\left(8x-4\right)\sqrt{x}-1=3x+2\sqrt{2x^2+5x-3}\)
<=> \(\left(4x^2-3x-1\right)+4\left(2x-1\right)\sqrt{x}-2\sqrt{\left(2x-1\right)\left(x+3\right)}\)
<=> \(\left(x-1\right)\left(4x+1\right)+2\sqrt{2x-1}\left(2\sqrt{x\left(2x-1\right)}-\sqrt{x+3}\right)=0\)
<=> \(\left(x-1\right)\left(4x+1\right)+2\sqrt{2x-1}.\frac{8x^2-4x-x-3}{2\sqrt{x\left(2x-1\right)}+\sqrt{x+3}}=0\)
<=>\(\left(x-1\right)\left(4x+1\right)+2\sqrt{2x-1}.\frac{\left(x-1\right)\left(8x+3\right)}{2\sqrt{x\left(2x-1\right)}+\sqrt{x+3}}=0\)
<=> \(\left(x-1\right)\left(4x+1+2\sqrt{2x-1}.\frac{8x+3}{2\sqrt{x\left(2x-1\right)}+\sqrt{x+3}}\right)=0\)
Với \(x\ge\frac{1}{2}\)thì \(4x+1+2\sqrt{2x-1}.\frac{8x-3}{2\sqrt{x\left(2x-1\right)}+\sqrt{x+3}}>0\)
=> \(x=1\)(TM ĐKXĐ)
Vậy x=1

Câu b bạn có bị lỗi dấu căn không mà sao nó kéo dài cả 2 vế pt vậy :v
\(a,\sqrt{x^2-6x+9}+x=11\\ \Leftrightarrow\sqrt{\left(x-3\right)^2}=11-x\)
\(\Leftrightarrow\left|x-3\right|=11-x\\ TH_1:x\ge3\\ x-3=11-x\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\left(tm\right)\)
\(TH_2:x< 3\\ -x+3=11-x\\ \Leftrightarrow-x+x=11-3\\ \Leftrightarrow0=8\left(VL\right)\)
Vậy \(S=\left\{7\right\}\)
\(c,\sqrt{16\left(x+1\right)}-\sqrt{9\left(x+1\right)}=4\) \(\left(dk:x\ge-1\right)\)
\(\Leftrightarrow\sqrt{4^2}.\sqrt{\left(x+1\right)}-\sqrt{3^2}.\sqrt{\left(x+1\right)}=4\left(1\right)\)
Đặt \(a=\sqrt{x+1}\left(a\ge0\right)\)
Pt trở thành : \(4a-3a=4\Leftrightarrow a=4\left(tmdk\right)\)
\(\Rightarrow\sqrt{x+1}=4\\ \Rightarrow\left(\sqrt{x+1}\right)^2=16\\ \Rightarrow\left|x+1\right|=16\)
\(TH_1:x\ge-1\\ x+1=16\Leftrightarrow x=15\left(tm\right)\\ TH_2:x< -1\\ -x-1=16\Leftrightarrow x=-17\left(tm\right)\)
Nhưng loại TH2 vì dk ban đầu là \(x\ge-1\)
Vậy \(S=\left\{15\right\}\)
\(d,\sqrt{9x+9}+\sqrt{4x+4}=\sqrt{x+1}\left(dk:x\ge-1\right)\\ \Leftrightarrow\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}-\sqrt{x+1}=0\)
Đặt \(\sqrt{x+1}=a\left(a\ge0\right)\)
Tới đây bạn làm tương tự câu c nha.

a: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(2x+3\right)^2}=5\)
=>|2x+3|=5
=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
b: ĐKXĐ: \(x\in R\)
\(\sqrt{9\left(x-2\right)^2}=18\)
=>\(\sqrt{9}\cdot\sqrt{\left(x-2\right)^2}=18\)
=>\(3\cdot\left|x-2\right|=18\)
=>\(\left|x-2\right|=6\)
=>\(\left[{}\begin{matrix}x-2=6\\x-2=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: x>=2
\(\sqrt{9x-18}-\sqrt{4x-8}+3\sqrt{x-2}=40\)
=>\(3\sqrt{x-2}-2\sqrt{x-2}+3\sqrt{x-2}=40\)
=>\(4\sqrt{x-2}=40\)
=>\(\sqrt{x-2}=10\)
=>x-2=100
=>x=102(nhận)
d: ĐKXĐ: \(x\in R\)
\(\sqrt{4\left(x-3\right)^2}=8\)
=>\(\sqrt{\left(2x-6\right)^2}=8\)
=>|2x-6|=8
=>\(\left[{}\begin{matrix}2x-6=8\\2x-6=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=14\\2x=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
e: ĐKXĐ: \(x\in R\)
\(\sqrt{4x^2+12x+9}=5\)
=>\(\sqrt{\left(2x\right)^2+2\cdot2x\cdot3+3^2}=5\)
=>\(\sqrt{\left(2x+3\right)^2}=5\)
=>|2x+3|=5
=>\(\left[{}\begin{matrix}2x+3=5\\2x+3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=2\\2x=-8\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)
f: ĐKXĐ:x>=6/5
\(\sqrt{5x-6}-3=0\)
=>\(\sqrt{5x-6}=3\)
=>\(5x-6=3^2=9\)
=>5x=6+9=15
=>x=15/5=3(nhận)

a) Ta có: \(\sqrt{25x+75}+3\sqrt{x-2}=2\sqrt{x-2}+\sqrt{9x-18}\)
\(\Leftrightarrow5\sqrt{x+3}+3\sqrt{x-2}=2\sqrt{x-2}+3\sqrt{x-2}\)
\(\Leftrightarrow\sqrt{25x+75}=\sqrt{4x-8}\)
\(\Leftrightarrow25x-4x=-8-75\)
\(\Leftrightarrow21x=-83\)
hay \(x=-\dfrac{83}{21}\)
b) Ta có: \(\sqrt{\left(2x-1\right)^2}=4\)
\(\Leftrightarrow\left|2x-1\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)
c) Ta có: \(\sqrt{\left(2x+1\right)^2}=3x-5\)
\(\Leftrightarrow\left|2x+1\right|=3x-5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=3x-5\left(x\ge-\dfrac{1}{2}\right)\\2x+1=5-3x\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3x=-5-1\\2x+3x=5-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\left(nhận\right)\\x=\dfrac{4}{5}\left(loại\right)\end{matrix}\right.\)
d) Ta có: \(\sqrt{4x-12}-14\sqrt{\dfrac{x-2}{49}}=\sqrt{9x-18}+8\)
\(\Leftrightarrow2\sqrt{x-3}-2\sqrt{x-2}=3\sqrt{x-2}+8\)
\(\Leftrightarrow2\sqrt{x-3}-5\sqrt{x-2}=8\)
\(\Leftrightarrow4\left(x-3\right)+25\left(x-2\right)-20\sqrt{x^2-5x+6}=8\)
\(\Leftrightarrow4x-12+25x-50-8=20\sqrt{\left(x-2\right)\left(x-3\right)}\)
\(\Leftrightarrow20\sqrt{\left(x-2\right)\left(x-3\right)}=29x-70\)
\(\Leftrightarrow x^2-5x+6=\dfrac{\left(29x-70\right)^2}{400}\)
\(\Leftrightarrow x^2-5x+6=\dfrac{841}{400}x^2-\dfrac{203}{20}x+\dfrac{49}{4}\)
\(\Leftrightarrow\dfrac{-441}{400}x^2+\dfrac{103}{20}x-\dfrac{25}{4}=0\)
\(\Delta=\left(\dfrac{103}{20}\right)^2-4\cdot\dfrac{-441}{400}\cdot\dfrac{-25}{4}=-\dfrac{26}{25}\)(Vô lý)
vậy: Phương trình vô nghiệm

1) \(\sqrt[]{9\left(x-1\right)}=21\)
\(\Leftrightarrow9\left(x-1\right)=21^2\)
\(\Leftrightarrow9\left(x-1\right)=441\)
\(\Leftrightarrow x-1=49\Leftrightarrow x=50\)
2) \(\sqrt[]{1-x}+\sqrt[]{4-4x}-\dfrac{1}{3}\sqrt[]{16-16x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}+\sqrt[]{4\left(1-x\right)}-\dfrac{1}{3}\sqrt[]{16\left(1-x\right)}+5=0\)
\(\)\(\Leftrightarrow\sqrt[]{1-x}+2\sqrt[]{1-x}-\dfrac{4}{3}\sqrt[]{1-x}+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}\left(1+3-\dfrac{4}{3}\right)+5=0\)
\(\Leftrightarrow\sqrt[]{1-x}.\dfrac{8}{3}=-5\)
\(\Leftrightarrow\sqrt[]{1-x}=-\dfrac{15}{8}\)
mà \(\sqrt[]{1-x}\ge0\)
\(\Leftrightarrow pt.vô.nghiệm\)
3) \(\sqrt[]{2x}-\sqrt[]{50}=0\)
\(\Leftrightarrow\sqrt[]{2x}=\sqrt[]{50}\)
\(\Leftrightarrow2x=50\Leftrightarrow x=25\)
1) \(\sqrt{9\left(x-1\right)}=21\) (ĐK: \(x\ge1\))
\(\Leftrightarrow3\sqrt{x-1}=21\)
\(\Leftrightarrow\sqrt{x-1}=7\)
\(\Leftrightarrow x-1=49\)
\(\Leftrightarrow x=49+1\)
\(\Leftrightarrow x=50\left(tm\right)\)
2) \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\) (ĐK: \(x\le1\))
\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}+5=0\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\) (vô lý)
Phương trình vô nghiệm
3) \(\sqrt{2x}-\sqrt{50}=0\) (ĐK: \(x\ge0\))
\(\Leftrightarrow\sqrt{2x}=\sqrt{50}\)
\(\Leftrightarrow2x=50\)
\(\Leftrightarrow x=\dfrac{50}{2}\)
\(\Leftrightarrow x=25\left(tm\right)\)
4) \(\sqrt{4x^2+4x+1}=6\)
\(\Leftrightarrow\sqrt{\left(2x+1\right)^2}=6\)
\(\Leftrightarrow\left|2x+1\right|=6\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=6\left(ĐK:x\ge-\dfrac{1}{2}\right)\\2x+1=-6\left(ĐK:x< -\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=5\\2x=-7\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\x=-\dfrac{7}{2}\left(tm\right)\end{matrix}\right.\)
5) \(\sqrt{\left(x-3\right)^2}=3-x\)
\(\Leftrightarrow\left|x-3\right|=3-x\)
\(\Leftrightarrow x-3=3-x\)
\(\Leftrightarrow x+x=3+3\)
\(\Leftrightarrow x=\dfrac{6}{2}\)
\(\Leftrightarrow x=3\)

Hung nguyen, Trần Thanh Phương, Sky SơnTùng, @tth_new, @Nguyễn Việt Lâm, @Akai Haruma, @No choice teen
help me, pleaseee
Cần gấp lắm ạ!
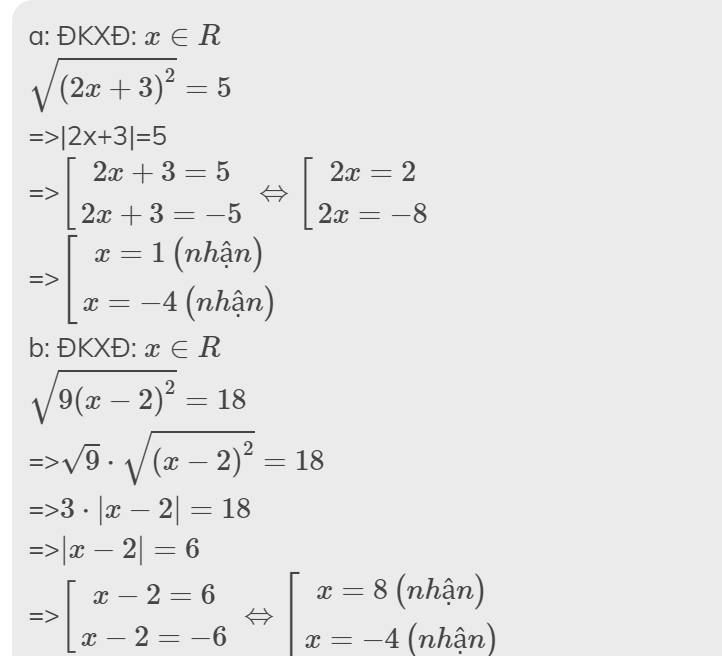
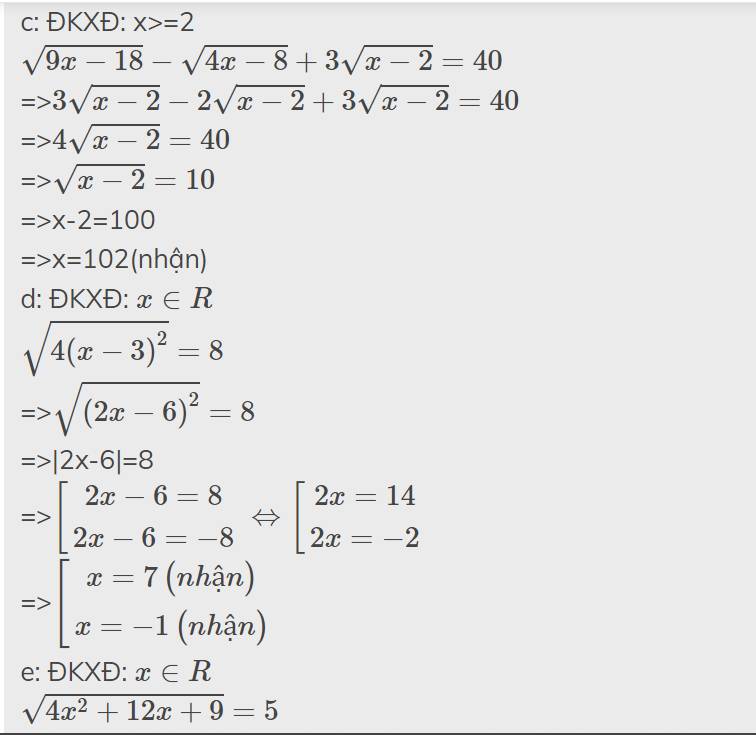
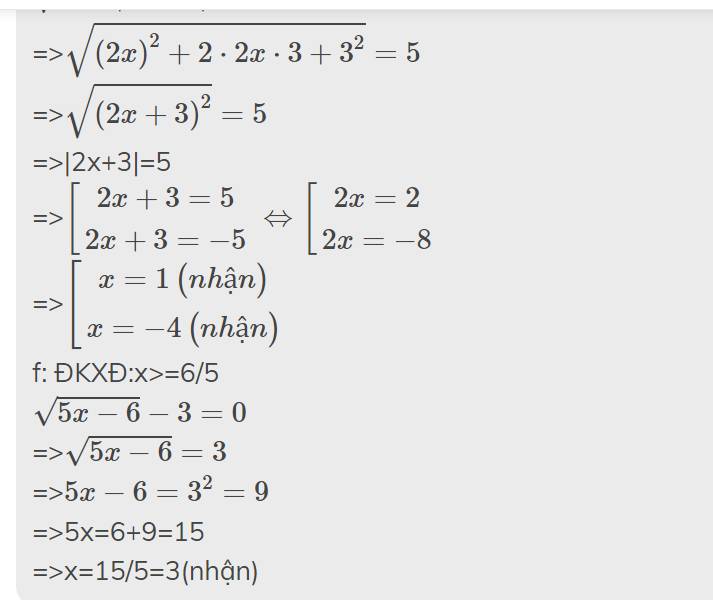
Câu 1 :
Xét điều kiện:\(\hept{\begin{cases}x\ge5\\x\le1\end{cases}}\)(Vô lý)
Vậy pt vô nghiệm
Câu 2 :
\(2\sqrt{x+2}+2\sqrt{x+2}-3\sqrt{x+2}=1\)\(\Leftrightarrow\sqrt{x+2}=1\Leftrightarrow x=-1\)
Vậy x=-1
Câu 3 :
\(\sqrt{3x^2-4x+3}=1-2x\)\(\Leftrightarrow3x^2-4x+3=1+4x^2-4x\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\sqrt{2}\)
Câu 4 :
\(4\sqrt{x+1}-3\sqrt{x+1}=4\Leftrightarrow\sqrt{x+1}=4\)
\(\Leftrightarrow x=15\)