
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>\(\widehat{AMB}=90^0\)
b: Xét ΔOMC vuông tại M có MH là đường cao
nên \(HC\cdot HO=HM^2\left(1\right)\)
Xét ΔMAB vuông tại M có MH là đường cao
nên \(HA\cdot HB=HM^2\left(2\right)\)
Từ (1) và (2) suy ra \(HC\cdot HO=HA\cdot HB\)
c: Xét tứ giác AMBQ có
O là trung điểm của AB và MQ
Do đó: AMBQ là hình bình hành
Hình bình hành AMBQ có AB=MQ
nên AMBQ là hình bình hành

1.4:
a: CH=16^2/24=256/24=32/3
BC=24+32/3=104/3
AC=căn 32/3*104/3=16/3*căn 13
b: BC=12^2/6=24
AC=căn 24^2-12^2=12*căn 3
CH=24-6=18

a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2

Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)


\(\left(3\sqrt{7}\right)^2=63>28=\left(\sqrt{28}\right)^2\) hoặc \(3\sqrt{7}>2\sqrt{7}=\sqrt{28}\)

3: \(=\dfrac{\left(3-\sqrt{5}\right)^2}{\sqrt{5}-3}=\sqrt{5}-3\)
4: \(=\dfrac{\left(\sqrt{5}-2\right)^2}{\sqrt{5}-2}=\sqrt{5}-2\)
5: \(=\dfrac{8-2\sqrt{15}+4\sqrt{15}}{\sqrt{5}+\sqrt{3}}\)
\(=\dfrac{8+2\sqrt{15}}{\sqrt{5}+\sqrt{3}}=\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{\sqrt{5}+\sqrt{3}}=\sqrt{5}+\sqrt{3}\)
6:
\(=\dfrac{8\sqrt{6}-11-4\sqrt{6}}{4\sqrt{2}-2\sqrt{3}}\)
\(=\dfrac{4\sqrt{6}-11}{4\sqrt{2}-2\sqrt{3}}=\dfrac{\sqrt{3}-2\sqrt{2}}{2}\)
1) \(\dfrac{3\sqrt{5}-5\sqrt{3}}{3-\sqrt{15}}=\dfrac{\sqrt{15}\left(\sqrt{3}-\sqrt{5}\right)}{\sqrt{3}\left(\sqrt{3}-\sqrt{5}\right)}=\sqrt{15}\)
2) \(\dfrac{5\sqrt{6}-6\sqrt{5}}{2\sqrt{15}-5\sqrt{2}}=\dfrac{\sqrt{30}\left(\sqrt{5}-\sqrt{6}\right)}{\sqrt{10}\left(\sqrt{6}-\sqrt{5}\right)}=-\sqrt{3}\)
3) \(\dfrac{14-6\sqrt{5}}{\sqrt{5}-3}=\dfrac{\left(3-\sqrt{5}\right)^2}{\sqrt{5}-3}=\sqrt{5}-3\)
4) \(\dfrac{9-4\sqrt{5}}{\sqrt{5}-2}=\dfrac{\left(2-\sqrt{5}\right)^2}{\sqrt{5}-2}=\sqrt{5}-2\)
5) \(\dfrac{\left(\sqrt{3}-\sqrt{5}\right)^2+4\sqrt{15}}{\sqrt{3}+\sqrt{5}}=\dfrac{\sqrt{3}+\sqrt{5}}{\sqrt{3}+\sqrt{5}}=1\)
6) \(\dfrac{8\sqrt{6}-\left(\sqrt{3}+2\sqrt{2}\right)^2}{4\sqrt{2}-2\sqrt{3}}=\dfrac{8\sqrt{6}-11-4\sqrt{6}}{4\sqrt{2}-2\sqrt{3}}\)
\(=\dfrac{4\sqrt{6}-11}{2\left(2\sqrt{2}-\sqrt{3}\right)}=\dfrac{(\sqrt{3}-2\sqrt{2})^2}{2\left(\sqrt{3}-2\sqrt{2}\right)}=\dfrac{\sqrt{3}-2\sqrt{2}}{2}\)



 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ


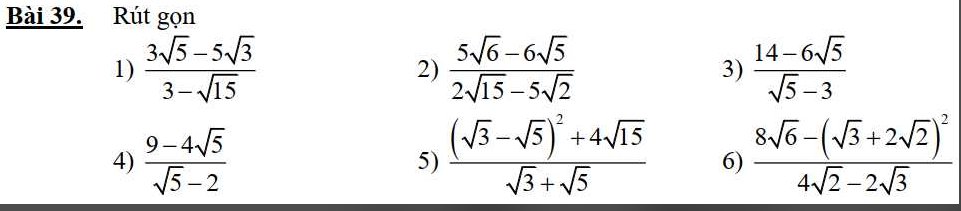 làm rõ ra giúp e ạ, e cảm ơn
làm rõ ra giúp e ạ, e cảm ơn
Xét (O) có
ΔMEN nội tiếp
MN là đường kính
Do đó: ΔMEN vuông tại E
=>\(\widehat{MEN}=90^0\)
=>\(\widehat{FEN}=90^0\)
Xét tứ giác HFEN có
\(\widehat{FHN}+\widehat{FEN}=90^0+90^0=180^0\)
=>HFEN là tứ giác nội tiếp
=>H,F,E,N cùng thuộc một đường tròn