
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=-20\\3a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=7\\b=8-3a=8-3\cdot7=-13\end{matrix}\right.\)

Bài 2:
a: Xét (O) có
\(\widehat{CBA}\) là góc tạo bởi tiếp tuyến dây cung chắn cung BC
\(\widehat{BDC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{CBA}=\widehat{BDC}\)
b: Xét ΔABC và ΔADB có
\(\widehat{ABD}=\widehat{ADB}\)
\(\widehat{A}\) chung
Do đó: ΔABC\(\sim\)ΔADB
Suy ra: AB/AD=AC/AB
hay \(AB^2=AC\cdot AD\)

3b.
\(\Delta=m^2+4\left(m+1\right)=\left(m+2\right)^2\)
Pt có 2 nghiệm pb khi \(\left(m+2\right)^2>0\Rightarrow m\ne-2\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=-\left(m+1\right)\end{matrix}\right.\)
\(x_1+x_2-2x_1x_2=8\)
\(\Leftrightarrow-m+2\left(m+1\right)=8\)
\(\Rightarrow m=6\) (thỏa mãn)
6.
\(M=x-\sqrt{x}+1=\left(x-\sqrt{x}+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(M_{min}=\dfrac{3}{4}\) khi \(\sqrt{x}=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{4}\)



5.1) Gọi \(A\left(x_A;y_A\right)\) là giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}y_A=2x_A+1\\y_A=-x_A+3\end{matrix}\right.\Rightarrow2x_A+1=-x_A+3\Rightarrow3x_A=2\Rightarrow x_A=\dfrac{2}{3}\)
\(\Rightarrow y_A=\dfrac{7}{3}\Rightarrow A\left(\dfrac{2}{3};\dfrac{7}{3}\right)\)
2) Vì \(\left(d_3\right)\) đi qua A nên \(\dfrac{7}{3}=\dfrac{2}{3}\left(m-1\right)+3m-2\Rightarrow\dfrac{7}{3}=\dfrac{11}{3}m-\dfrac{8}{3}\)
\(\Rightarrow\dfrac{11}{3}m=5\Rightarrow m=\dfrac{15}{11}\)
3) Gọi \(B\left(x_B;y_B\right)\) là giao điểm của \(\left(d_1\right)\) và \(\left(d_3\right)\)
Vì \(B\in Ox\Rightarrow y_B=0\)
Vì \(B\in\left(d_1\right)\Rightarrow y_B=2x_B+1\Rightarrow0=2x_B+1\Rightarrow x_B=-\dfrac{1}{2}\)
\(\Rightarrow B\left(-\dfrac{1}{2};0\right)\Rightarrow0=-\dfrac{1}{2}\left(m-1\right)+3m-2\Rightarrow0=\dfrac{5}{2}m-\dfrac{3}{2}\)
\(\Rightarrow\dfrac{5}{2}m=\dfrac{3}{2}\Rightarrow m=\dfrac{3}{5}\)
c) Gọi \(C\left(x_C;y_C\right)\) là giao điểm của \(\left(d_2\right)\) và \(\left(d_3\right)\)
Vì \(C\in Oy\Rightarrow x_C=0\)
Vì \(B\in\left(d_2\right)\Rightarrow y_B=-x_B+3\Rightarrow y_B=3\Rightarrow C\left(0;3\right)\)
\(\Rightarrow3=3m-2\Rightarrow3m=5\Rightarrow m=\dfrac{5}{3}\)





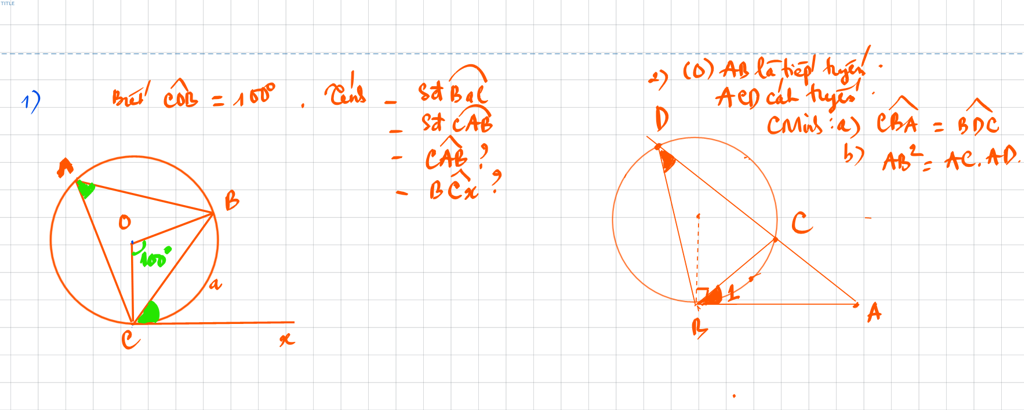
 giúp e bài 3b và bài 6 vs ạ
giúp e bài 3b và bài 6 vs ạ




1 Câu cx đc ạ
Câu 1:
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b\ne-3\\\dfrac{1}{2}a+b=\dfrac{5}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{5}{2}-1=\dfrac{3}{2}\end{matrix}\right.\\ \Leftrightarrow y=2x+\dfrac{3}{2}\)