K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 11 2021
a) \(\Rightarrow\left|\dfrac{3}{4}+x\right|=0\Rightarrow\dfrac{3}{4}+x=0\Rightarrow x=-\dfrac{3}{4}\)
b) \(\Rightarrow x+0,4=\dfrac{4}{9}:\dfrac{2}{3}=\dfrac{2}{3}\Rightarrow x=\dfrac{2}{3}-0,4=\dfrac{4}{15}\)
NG
18 tháng 1 2021
Lấy điểm D sao cho điểm F là trung điểm của DE\(\Rightarrow\)\(EF=DF=\dfrac{1}{2}DE\), nối E với C
\(\text{Xét }\Delta AEF\text{ và }\Delta CDF\text{ có:}\)
\(AF=FC\left(gt\right)\left(1\right)\)
\(\widehat{F_1}=\widehat{F_2}\left(\text{đối đỉnh}\right)\left(2\right)\)
\(EF=DF\left(\text{hình vẽ}\right)\left(3\right)\)
\(\text{Từ (1),(2) và (3)}\Rightarrow\Delta AEF=\Delta CDF\left(c.g.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}AE=CD\left(\text{2 cạnh tương ứng}\right),\text{mà }AE=BE\left(gt\right)\Rightarrow BE=CD\\\widehat{EAF}=\widehat{DCF}\left(\text{2 góc tương ứng}\right)\left(5\right)\end{matrix}\right.\)
\(\text{Mà 2 góc này ở vị trí so le trong của đường thẳng AE và CD}\left(6\right)\)
\(\text{Từ (5) và (6)}\Rightarrow AE\text{//}CD\left(\text{dấu hiệu nhận biết}\right)\)
\(\text{Hay }BE\text{//}CD\left(\text{do A,E,B thẳng hàng}\right)\)
\(\Rightarrow\widehat{BEC}=\widehat{DCE}\left(\text{so le trong}\right)\)
\(\text{Xét }\Delta BEC\text{ và }\Delta DCE\text{ có:}\)
\(BE=DC\left(cmt\right)\left(7\right)\)
\(\widehat{BEC}=\widehat{DCE}\left(cmt\right)\left(8\right)\)
\(\text{CE chung}\left(9\right)\)
\(\text{Từ (7),(8) và (9)}\Rightarrow\Delta BEC=\Delta DCE\left(c.g.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}BC=DE\left(\text{2 cạnh tương ứng}\right),\text{Mà }EF=\dfrac{1}{2}DE\Rightarrow EF=\dfrac{1}{2}BC\Rightarrow EF=\dfrac{BC}{2}\left(đpcm\right)\\\widehat{BCE}=\widehat{DEC}\left(\text{2 góc tương ứng}\right)\text{Hay }\widehat{BCE}=\widehat{FEC}\left(10\right)\end{matrix}\right.\)
\(\text{Mà 2 góc này ở vị trí so le trong của 2 đường thẳng BC và EF}\left(11\right)\)
\(\text{Từ (10) và (11)}\Rightarrow BC\text{//}EF\left(\text{dấu hiệu nhận biết}\right)\left(đpcm\right)\)
4 tháng 8 2021
\(A\left(x\right)+B\left(x\right)=3x^4-4x^3+2x^2-3+8x^4+x^3-9x+\dfrac{2}{5}\)
\(=11x^4-3x^3+2x^2-9x-\dfrac{13}{5}\)
\(A\left(x\right)-B\left(x\right)=3x^4-4x^3+2x^2-3-8x^4-x^3+9x-\dfrac{2}{5}\)
\(=-5x^4-5x^3+2x^2+9x-\dfrac{17}{5}\)
\(B\left(x\right)-A\left(x\right)=8x^4+x^3-9x+\dfrac{2}{5}-3x^4+4x^3-2x^2+3\)
\(=5x^4+5x^3-2x^2-9x+\dfrac{17}{5}\)
4 tháng 8 2021
a) Ta có: \(P\left(x\right)=3x^5-2x^4-2x^5-2x^2-x+3x^2+2\)
\(=x^5-2x^4+x^2+2\)
Ta có: \(Q\left(x\right)=x^5+8-5x+3x^3+3x+x^4-4x^5\)
\(=-3x^5+x^4+3x^3-2x+8\)
b) \(P\left(x\right)+Q\left(x\right)=x^5-2x^4+x^2+2-3x^5+x^4+3x^3-2x+8\)
\(=-2x^5-x^4+3x^3+x^2-2x+10\)
\(P\left(x\right)-Q\left(x\right)=x^5-2x^4+x^2+2+3x^5-x^4-3x^3+2x-8\)
\(=4x^5-3x^4-3x^3+x^2+2x-6\)
26 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a)`
\(3^{200}\text{ và }2^{300}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=\left(2^3\right)^{100}=8^{100}\)
Vì `9 > 8 => 9^100 > 8^100`
`=> 3^200 > 2^300`
`b)`
\(27^{101}\text{ và }81^{35}\)
\(27^{101}=\left(3^3\right)^{101}=3^{303}\)
\(81^{35}=\left(3^4\right)^{35}=3^{140}\)
Vì `303 > 140 => 3^303 > 3^140`
`=> 27^101 > 81^35`
`c)`
\(2^{332}\text{ và }3^{223}\)
\(2^{332}< 2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{223}>3^{222}=\left(3^2\right)^{111}=9^{111}\)
Vì `9 > 8 => 9^111 > 8^111`
`=> 2^332 < 3^223.`
26 tháng 6 2023
a: 3^200=9^100
2^300=8^100
mà 9>8
nên 3^200>2^300
b: 27^101=3^303
81^35=3^140
mà 303>140
nên 27^101>81^35
c: 2^332<2^333=8^111
3^223>3^222=9^111
mà 9>8
nên 3^223>8^111>2^332
26 tháng 9 2021
Đặt \(\dfrac{x}{4}=\dfrac{y}{7}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=7k\end{matrix}\right.\)
Ta có: xy=112
\(\Leftrightarrow28k^2=112\)
\(\Leftrightarrow k^2=4\)
Trường hợp 1: k=2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot2=8\\y=7k=7\cdot2=14\end{matrix}\right.\)
Trường hợp 2: x=-2
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-8\\y=7k=-14\end{matrix}\right.\)
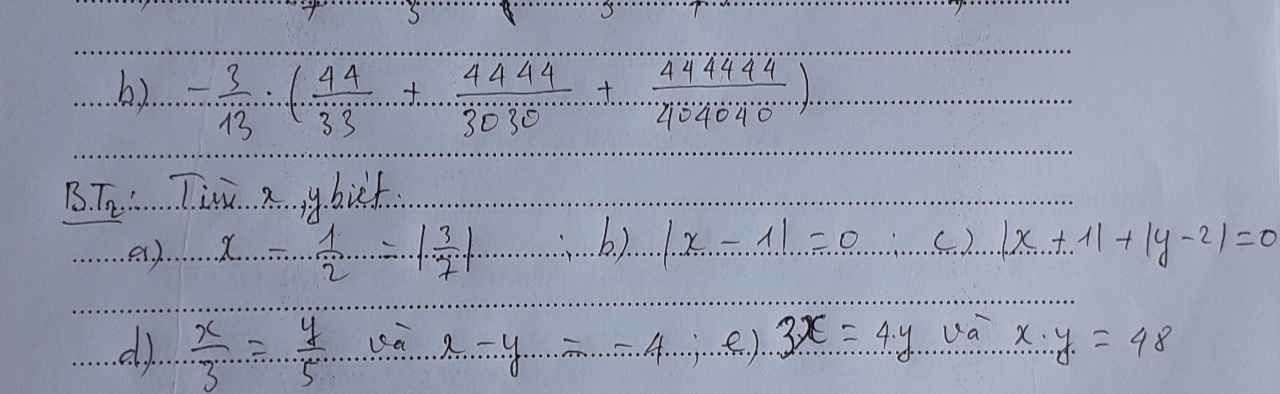
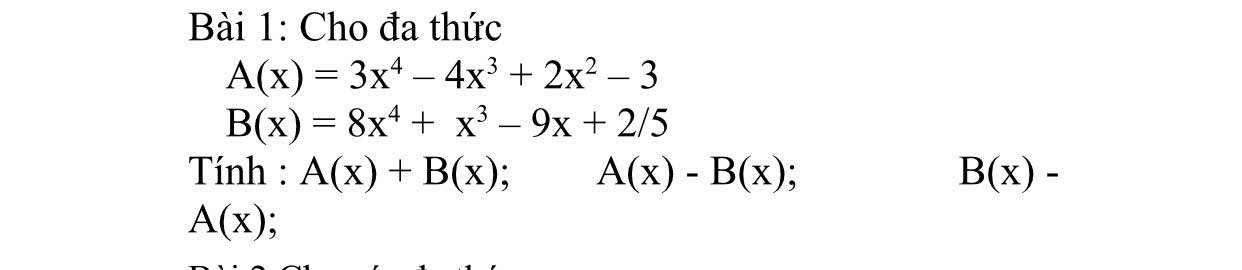
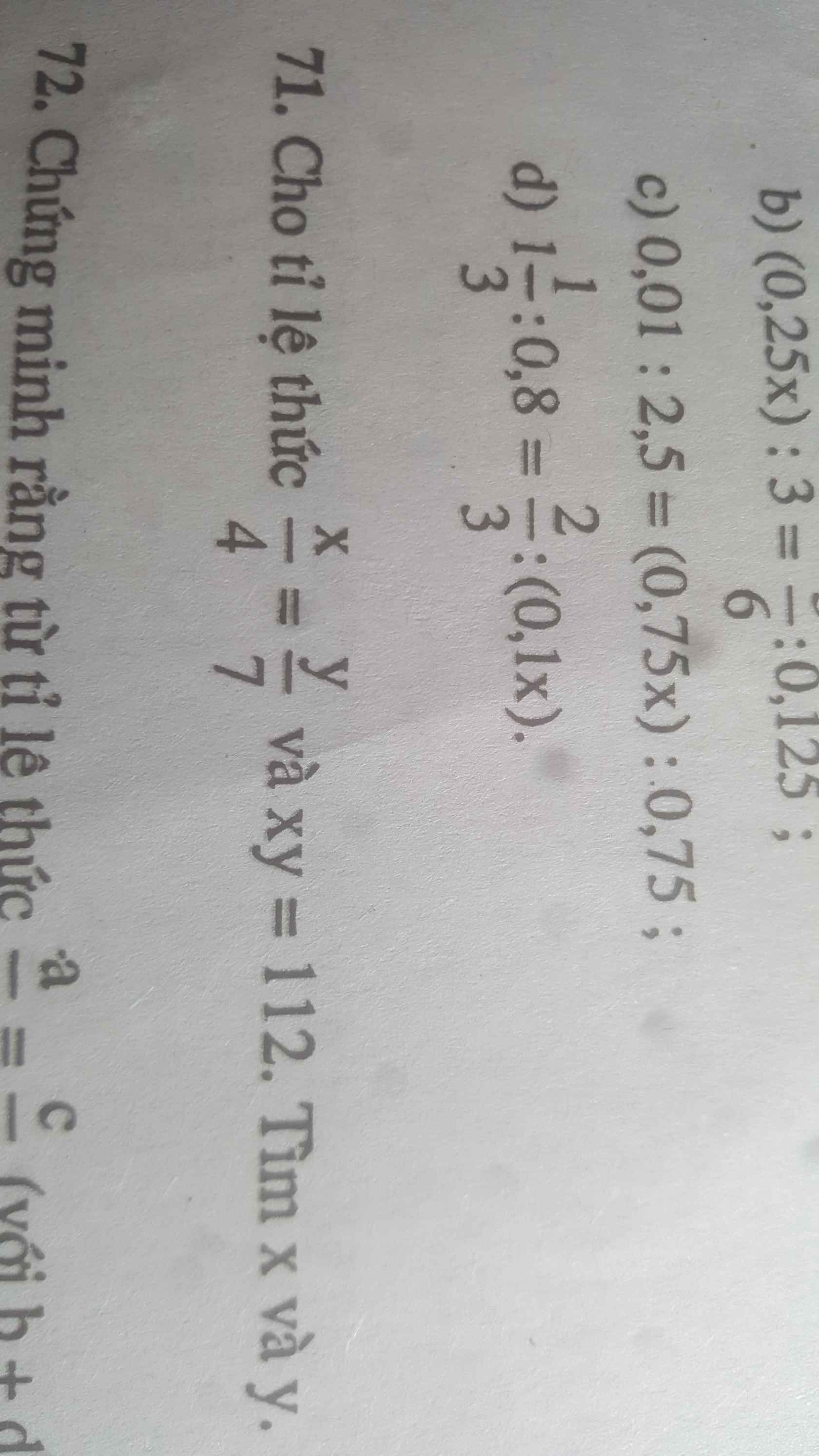
a) Ta có: \(x-\dfrac{1}{2}=\left|\dfrac{3}{7}\right|\)
nên \(x-\dfrac{1}{2}=\dfrac{3}{7}\)
hay \(x=\dfrac{3}{7}+\dfrac{1}{2}=\dfrac{6}{14}+\dfrac{7}{14}=\dfrac{13}{14}\)
b) Ta có: |x-1|=0
nên x-1=0
hay x=1
c) Ta có: \(\left|x+1\right|\ge0\forall x\)
\(\left|y-2\right|\ge0\forall y\)
Do đó: \(\left|x+1\right|+\left|y-2\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=-1 và y=2
d) Ta có: \(\dfrac{x}{3}=\dfrac{y}{5}\)
mà x-y=-4
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x-y}{3-5}=\dfrac{-4}{-2}=2\)
Do đó: x=6; y=10
e) Ta có: 3x=4y
nên \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}\)
Đặt \(\dfrac{x}{\dfrac{1}{3}}=\dfrac{y}{\dfrac{1}{4}}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k\\y=\dfrac{1}{4}k\end{matrix}\right.\)
Ta có: xy=48
nên \(\dfrac{1}{3}k\cdot\dfrac{1}{4}k=48\)
\(\Leftrightarrow k^2\cdot\dfrac{1}{12}=48\)
\(\Leftrightarrow k^2=48\cdot12=576\)
hay \(k\in\left\{24;-24\right\}\)
Trường hợp 1: k=24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot24=8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot24=6\end{matrix}\right.\)
Trường hợp 2: k=-24
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}k=\dfrac{1}{3}\cdot\left(-24\right)=-8\\y=\dfrac{1}{4}k=\dfrac{1}{4}\cdot\left(-24\right)=-6\end{matrix}\right.\)