Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)

Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn

Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):

Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)

\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)

Do đó:

\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)

ĐKXĐ cho căn thức: \(x\ge-\dfrac{1}{2}\)

\(\lim\limits_{x\rightarrow+\infty}\dfrac{3x+1-\sqrt{2x+1}}{x^2-x}=\lim\limits_{x\rightarrow+\infty}\dfrac{\dfrac{3}{x}+\dfrac{1}{x^2}-\sqrt{\dfrac{2}{x^3}+\dfrac{1}{x^4}}}{1-\dfrac{1}{x}}=\dfrac{0}{1}=0\)

\(\Rightarrow y=0\) là TCN

\(\lim\limits_{x\rightarrow0}\dfrac{3x+1-\sqrt{2x+1}}{x^2-x}=\lim\limits_{x\rightarrow0}\dfrac{9x^2+4x}{x\left(x-1\right)\left(3x+1+\sqrt{2x+1}\right)}=\lim\limits_{x\rightarrow0}\dfrac{9x+4}{\left(x-1\right)\left(3x+1+\sqrt{2x+1}\right)}\)

\(=\dfrac{4}{-1\left(1+1\right)}\) hữu hạn

\(\Rightarrow x=0\) không phải tiệm cận

\(\lim\limits_{x\rightarrow1}\dfrac{3x+1-\sqrt{2x+1}}{x\left(x-1\right)}=\dfrac{4-\sqrt{3}}{0}=+\infty\Rightarrow x=1\) là TCĐ

Đồ thị hàm số có 2 tiệm cận

Từ đề bài ta suy ra tất cả các mặt bên của hộp đều là hình thoi (được ghép từ 2 tam giác đều)

\(\Rightarrow A'D=A'B=A'A=a\Rightarrow\) hình chiếu vuông góc của A' lên (ABCD) trùng trọng tâm E của tam giác ABD

\(\widehat{DBE}=\dfrac{1}{2}.60^0=30^0\Rightarrow\widehat{CBE}=\widehat{CBD}+\widehat{DBE}=60^0+30^0=90^0\)

\(\Rightarrow BC\perp BE\)

Mà \(A'E\perp\left(ABCD\right)\Rightarrow A'E\perp BC\)

\(\Rightarrow BC\perp\left(A'BE\right)\Rightarrow BC\perp A'B\)

\(\Rightarrow B'C'\perp A'B\)

\(AE=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'E=\sqrt{A'A^2-AE^2}=\dfrac{a\sqrt{6}}{3}\)

Qua C' dựng đường thẳng song song A'E cắt AC tại F \(\Rightarrow C'F=A'E=\dfrac{a\sqrt{6}}{3}\)

\(CF=AE=\dfrac{a\sqrt{3}}{3}\) ; \(AC=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\Rightarrow AF=AC+CF=\dfrac{4a\sqrt{3}}{3}\)

\(\Rightarrow AC'=\sqrt{AF^2+C'F^2}=a\sqrt{6}\)

\(CP=\dfrac{1}{3}CC'\) ; \(CN=\dfrac{1}{3}BC\)

Nối PN kéo dài cắt BB' tại J

Talet: \(\dfrac{CP}{BJ}=\dfrac{CN}{NB}=\dfrac{1}{2}\Rightarrow BJ=2CP=\dfrac{2a}{3}\Rightarrow\dfrac{BJ}{B'J}=\dfrac{\dfrac{2a}{3}}{a+\dfrac{2a}{3}}=\dfrac{2}{5}\)

Nối JM cắt A'B' kéo dài tại K

Talet: \(\dfrac{BM}{B'K}=\dfrac{BJ}{B'J}=\dfrac{2}{5}\Rightarrow B'K=\dfrac{5BM}{2}=\dfrac{5a}{4}\)

Nối MN cắt BD tại H và cắt CD tại G

Talet: \(\dfrac{CG}{BM}=\dfrac{CN}{BN}=\dfrac{1}{2}\Rightarrow CG=\dfrac{1}{2}BM=\dfrac{a}{4}\Rightarrow DG=a+\dfrac{a}{4}=\dfrac{5a}{4}\)

Talet: \(\dfrac{BH}{DH}=\dfrac{BM}{DG}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (1)

Nối GP cắt C'D' tại Q

Talet: \(\dfrac{CG}{C'Q}=\dfrac{CP}{C'P}=\dfrac{1}{2}\Rightarrow C'Q=2CG=\dfrac{a}{2}\)

Nối QK cắt B'D' tại L

Talet: \(\dfrac{D'L}{B'L}=\dfrac{D'Q}{B'K}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (2)

(1);(2) \(\Rightarrow D'L=BH\) (do \(BD=B'D'\))

Nối HL cắt BD' tại I

Talet: \(\dfrac{D'I}{IB}=\dfrac{D'L}{BH}=1\)

Gọi F là giao điểm QK và A'D', O là giao điểm JK và A'A

Ta đồng thời suy ra luôn NPQFOM là thiết diện của (MNP) và chóp

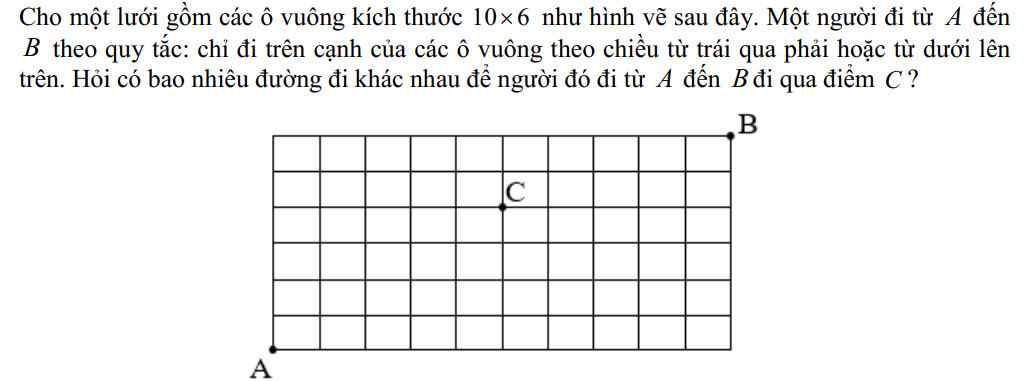
Từ A đến C, có 4 đoạn đi lên (nằm song song nhau) và 5 đoạn đi ngang nằm song song

Ta kí hiệu đi lên là L và đi ngang là N, như vậy, số cách đi từ A đến C là số cách sắp xếp 9 kí tự bao gồm 4L và 5N

\(\Rightarrow\) Có \(\dfrac{9!}{5!.4!}\) cách

Tương tự, từ C đến B có 2L và 5N, có \(\dfrac{7!}{2!.5!}\) cách

Tổng cộng: \(\dfrac{9!}{5!.4!}.\dfrac{7!}{2!.5!}\) cách đi từ A đến B

em cảm ơn thầyyyyyyyy

câu 2a đó ạ

dùng ông thức hạ bậc

cos²a=\(\dfrac{1+cos2a}{2}\)

pt<=>1+cos(4x+\(\dfrac{2\Pi}{3}\))-3sin(2x+\(\dfrac{5\Pi}{6}\))+1=0

<=>-\(\dfrac{1}{2}\)cos4x-\(\dfrac{\sqrt{3}}{2}\)sin4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x-\(\dfrac{3}{2}\)cos2x+2=0

<=>(-\(\dfrac{1}{2}\)cos4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)+(-\(\sqrt{3}\)sin2x.cos2x-\(\dfrac{3}{2}\)cos2x)=0

<=>[-\(\dfrac{1}{2}\)(1-2sin²2x)+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0

<=>(sin²2x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+\(\dfrac{3}{2}\))-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0

<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x+\(\sqrt{3}\))-cos2x.(sin2x+\(\dfrac{\sqrt{3}}{2}\))=0

<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x-cos2x+\(\sqrt{3}\))=0

tới đây bạn tự giải nhé

Câu b đề sai, hai mặt phẳng (SAC) và (SBD) không hề vuông góc với nhau (chúng chỉ vuông góc trong trường hợp ABCD là hình vuông)

Do câu b đề sai, (SAC) và (SBD) không vuông góc nên câu c rất khó tính :(

Từ A, kẻ \(AH\perp\left(SBD\right)\)

Gọi K là điểm đối xứng H qua O \(\Rightarrow\) AHCK là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm)

\(\Rightarrow\left\{{}\begin{matrix}CK//AH\\CK=AH\end{matrix}\right.\Rightarrow CK\perp\left(SBD\right)\) (K đương nhiên thuộc (SBD) do H, O đều thuộc (SBD))

\(\Rightarrow\widehat{CSK}\) là góc cần tìm

Trong mp (SBD), nối B và H kéo dài cắt SD tại E

\(\left\{{}\begin{matrix}SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp SD\) (1)

Mà \(AH\perp\left(SBD\right)\Rightarrow AH\perp SD\) (2)

(1);(2) \(\Rightarrow SD\perp\left(ABE\right)\Rightarrow SD\perp AE\)

Áp dụng hệ thức lượng trong tam giác vuông SAD:

\(\frac{1}{AE^2}=\frac{1}{SA^2}+\frac{1}{AD^2}\)

Áp dụng hệ thức lượng trong tam giác vuông ABE:

\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AE^2}=\frac{1}{AB^2}+\frac{1}{SA^2}+\frac{1}{AD^2}=\frac{1}{a^2}+\frac{1}{9a^2}+\frac{1}{4a^2}\Rightarrow AH=\frac{6a}{7}\)

Số đẹp quá ta :D

\(\Rightarrow CK=\frac{6a}{7}\)

Lại có:

\(SC=\sqrt{SA^2+AC^2}=\sqrt{SA^2+AB^2+BC^2}=a\sqrt{14}\)

\(\Rightarrow sin\widehat{CSK}=\frac{CK}{SC}=\frac{6}{7\sqrt{14}}\)

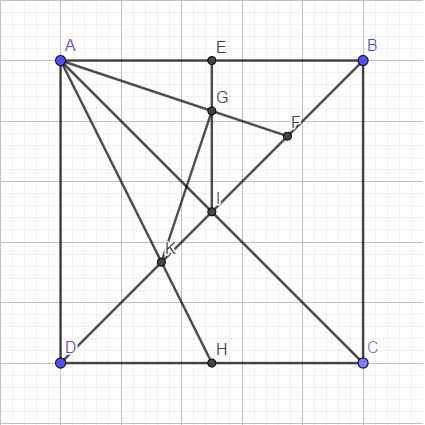
Đặt tên điểm như hình vẽ bên dưới

Ta có: F là trung điểm BI \(\Rightarrow\overrightarrow{AF}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)\)

\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AF}=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{AI}\right)=\dfrac{1}{3}\left(\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AC}\)

\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{6}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\)

\(\overrightarrow{AH}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}\)

\(\Rightarrow\overrightarrow{AK}=\dfrac{2}{3}\overrightarrow{AH}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\)

\(\overrightarrow{GK}=\overrightarrow{GA}+\overrightarrow{AK}=-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{6}\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}=-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)

\(\Rightarrow\overrightarrow{AG}.\overrightarrow{GK}=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)=-\dfrac{1}{12}AB^2+\dfrac{1}{12}AD^2=0\)

\(\Rightarrow AG\perp GK\)

\(\left\{{}\begin{matrix}\overrightarrow{GA}=\left(a+\dfrac{1}{3};b\right)\\\overrightarrow{KG}=\left(0;\dfrac{5}{3}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{GA}.\overrightarrow{KG}=\left(a+\dfrac{1}{3}\right).0+\dfrac{5}{3}b=0\Rightarrow b=0\)

Mặt khác: \(AG^2-GK^2=\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{6}\overrightarrow{AD}\right)^2-\left(-\dfrac{1}{6}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\right)^2=0\)

\(\Rightarrow AG^2=GK^2\Rightarrow\left(a+\dfrac{1}{3}\right)^2=\left(\dfrac{5}{3}\right)^2\Rightarrow a=-2\)