
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. \(\sqrt{\left(2+\sqrt{7}\right)^2}=2+\sqrt{7}=2\dfrac{\sqrt{7}}{1}\)
c. \(5\sqrt{x^2-6x+9}=5\sqrt{\left(x-3\right)^2}=5\left(x-3\right)=5x-15\)
d. \(\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-7\right)^2}=2-\sqrt{5}+\sqrt{5}-7=-5\)
a) \(\sqrt{\left(2+\sqrt{7}\right)^2}=\left|2+\sqrt{7}\right|=2+\sqrt{7}\)
b) \(\sqrt{4+2\sqrt{3}}=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
c) \(5\sqrt{x^2-6x+9}=5\sqrt{\left(x-3\right)^2}=5\left|x-3\right|=5\left(3-x\right)=15-5x\)(do x<3)
d) \(\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}-7\right)^2}=2-\sqrt{5}+\sqrt{5}-7=-5\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{1}{2}\\x_1x_2=-2\end{matrix}\right.\)
\(A=3-x_1^2-x_2^2\\ =3-\left(x_1^2+x_2^2\right)\\ =3-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =3-\left[\left(-\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =3-\left(\dfrac{1}{4}+4\right)\\ =3-\dfrac{17}{4}\\ =-\dfrac{5}{4}\)
\(B=\left(x_1-x_2\right)^2\\ =x_1^2+x_2^2-2x_1x_2\\ =\left(x_1+x_2\right)^2-4x_1x_2\\ =\left(\dfrac{1}{2}\right)^2-4.\left(-2\right)\\ =\dfrac{1}{4}+8\\ =\dfrac{33}{4}\)
\(D=\left(1+x_1\right)\left(2-x_1\right)+\left(1+x_2\right)\left(2-x_2\right)\\ =2+x_1-x_1^2+2+x_2-x_2^2\\ =4+\left(x_1+x_2\right)-\left(x_1^2+x_2^2\right)\\ =4+\dfrac{1}{2}-\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\dfrac{9}{2}-\left[\left(\dfrac{1}{2}\right)^2-2.\left(-2\right)\right]\\ =\dfrac{9}{2}-\dfrac{17}{4}\\ =\dfrac{1}{4}\)

1: \(A=\dfrac{\left(x+1\right)^3}{\left(x+1\right)^2}=x+1\)
\(B=\dfrac{\left(x+1\right)\cdot\left(x^2-x+1\right)}{x+1}=x^2-x+1\)
2: A=B
=>x^2-x+1=x+1
=>x^2-2x=0
=>x=0 hoặc x=2

1:
1: =2căn 3-3căn 3+4căn 3=3căn 3
2: =(3căn 5+2căn 5-4căn 5)/căn 5=1
3: =6căn 3-4/3*căn 3-4*căn 3-5/3*căn 3
=-căn 3
4: =(2căn 7-2căn 14+căn 7)*căn 7+14căn 2
=21
5:
\(=\left(3\sqrt{5}-2\sqrt{3}\right)\left(3\sqrt{5}+2\sqrt{3}\right)=45-12=33\)
6: \(=\left(6\sqrt{5}-5\sqrt{5}-3\sqrt{5}\right)\cdot\sqrt{5}\)
=-2căn 5*căn 5=-10
7:
\(=\dfrac{6\cdot8\sqrt{2}-\dfrac{3}{5}\cdot5\sqrt{2}+14\sqrt{2}}{3\sqrt{2}}=16-1+\dfrac{14}{3}=15+\dfrac{14}{3}=\dfrac{59}{3}\)
8: \(=\left(8\sqrt{3}-\sqrt{3}+3\sqrt{3}\right)\cdot2\sqrt{3}\)
=60
11:
=2+căn 3-2+căn 3=2*căn 3

a: \(\dfrac{1}{\sqrt{n}}=\dfrac{2}{\sqrt{n}+\sqrt{n}}< \dfrac{2}{\sqrt{n}+\sqrt{n-1}}\)
\(=2\left(\sqrt{n}-\sqrt{n-1}\right)\)
\(\dfrac{1}{\sqrt{n}}=\dfrac{2}{\sqrt{n}+\sqrt{n}}>\dfrac{2}{\sqrt{n}+\sqrt{n+1}}=2\left(\sqrt{n+1}-\sqrt{n}\right)\)
=>\(2\left(\sqrt{n+1}-\sqrt{n}\right)< \dfrac{1}{\sqrt{n}}< 2\left(\sqrt{n}-\sqrt{n-1}\right)\)
b: 2(căn 101-căn 2)<1/căn 2+1/căn 3+...+1/căn 100<2(căn 100-căn 1)=18
2(căn 101-căn 2)=2căn 101-2căn 2>2căn 100-3=17
=>\(17< \dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{100}}< 18\)

a:
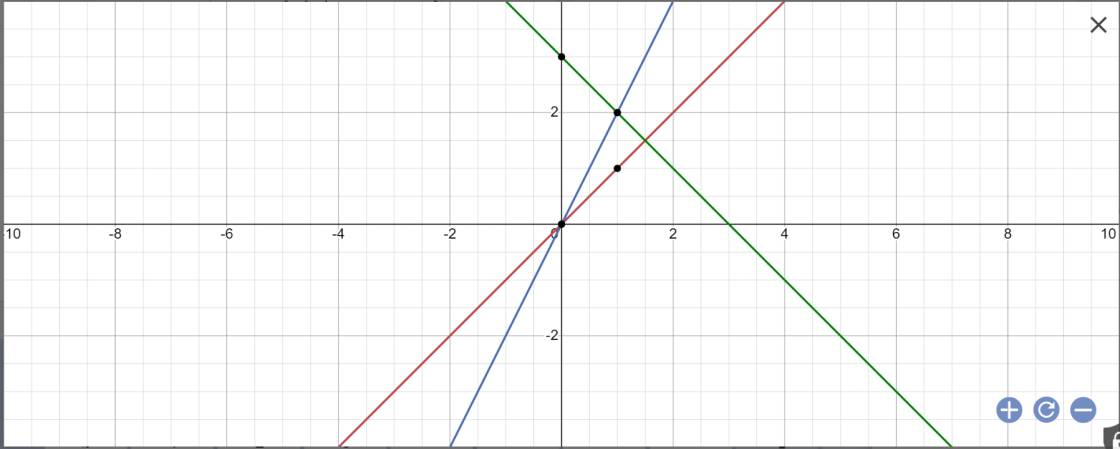
b: Tọa độ A là:
x=-x+3 và y=x
=>x=3/2 và y=3/2
=>A(1,5;1,5)
Tọa độ B là:
2x=-x+3 và y=2x
=>3x=3 và y=2x
=>x=1 và y=2
=>B(1;2)
O(0;0): A(1,5;1,5); B(1;2)
\(OA=\sqrt{1.5^2+1.5^2}=\dfrac{3}{2}\sqrt{2}\)
\(OB=\sqrt{1^2+2^2}=\sqrt{5}\)
\(AB=\sqrt{\left(1-1.5\right)^2+\left(2-1.5\right)^2}=\dfrac{\sqrt{2}}{2}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{3}{\sqrt{10}}\)
=>\(sinAOB=\dfrac{1}{\sqrt{10}}\)
\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB\cdot sinAOB=\dfrac{1}{2}\cdot\dfrac{1}{\sqrt{10}}\cdot\dfrac{3}{\sqrt{10}}=\dfrac{3}{2}\)

a: \(Q=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}-2-x+\sqrt{x}+2}{x-1}\cdot\dfrac{1}{\sqrt{x}}=\dfrac{2}{x-1}\)
b: |Q|>-Q
=>|Q|+Q>0
=>Q>0
=>\(\dfrac{2}{x-1}>0\)
=>x-1>0
=>x>1
c: Để Q nguyên thì \(2⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2\right\}\)
=>\(x\in\left\{2;0;3;-1\right\}\)
mà x>0 và x<>1
nên \(x\in\left\{2;3\right\}\)

Hình vẽ nhỏ quá. Bạn nên gõ đề bằng công thức toán để được hỗ trợ tốt hơn.

a: Ta có: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=3^2+4^2=25\)
=>\(BC=\sqrt{25}=5\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot5=3\cdot4=12\)
=>\(AH=\dfrac{12}{5}=2,4\left(cm\right)\)
b: Ta có: ΔOAC cân tại O
mà OM là đường trung tuyến
nên OM\(\perp\)AC tại M và OM là phân giác của \(\widehat{AOC}\)
Xét tứ giác AHOM có
\(\widehat{AHO}+\widehat{AMO}=90^0+90^0=180^0\)
=>AHOM là tứ giác nội tiếp đường tròn đường kính AO
=>A,H,M,O cùng thuộc đường tròn tâm I, đường kính AO
c: Xét ΔOCN và ΔOAN có
OC=OA(=R)
\(\widehat{CON}=\widehat{AON}\)(ON là phân giác của góc AOC)
ON chung
Do đó: ΔOCN=ΔOAN
=>\(\widehat{OCN}=\widehat{OAN}=90^0\)
=>NA\(\perp\)AO tại A
Xét (I) có
AO là đường kính
NA\(\perp\)AO tại A
Do đó: NA là tiếp tuyến của (I)
=>NA là tiếp tuyến của đường tròn ngoại tiếp ΔHMO
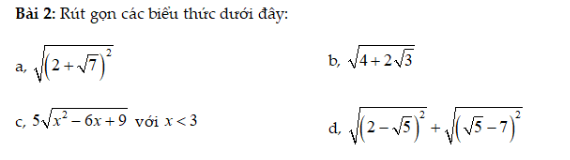

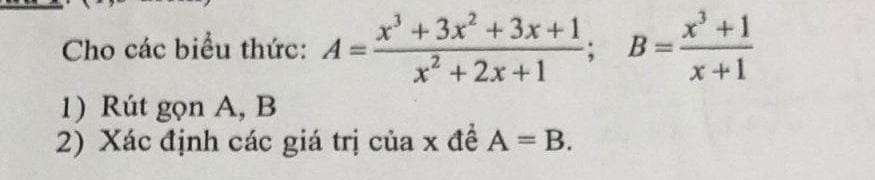

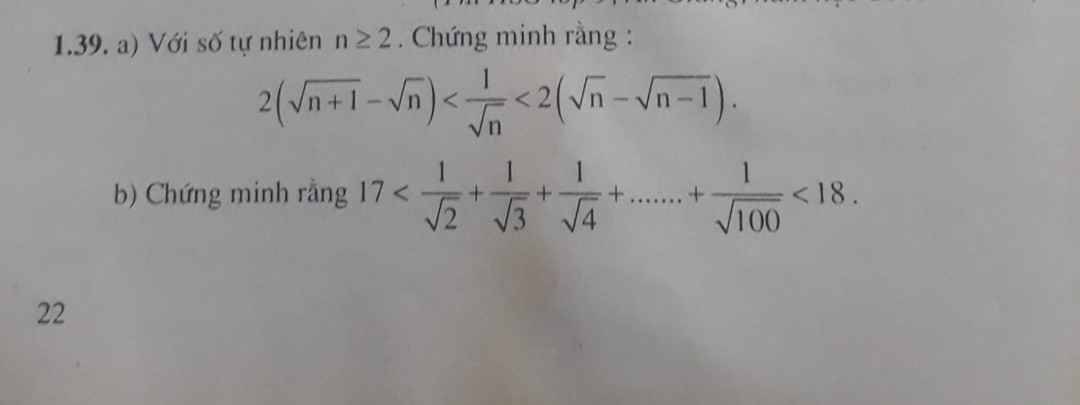
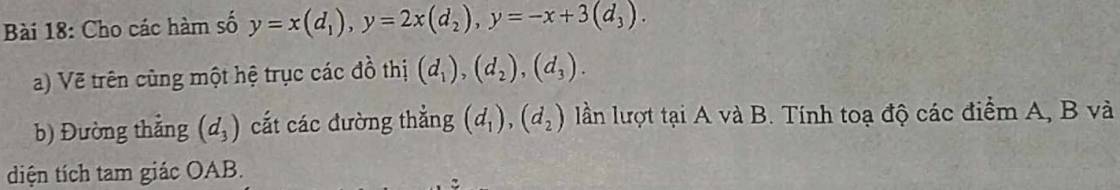 giup mik voi
giup mik voi giup mik voi
giup mik voi
 X
X
 Giup to aaaaa
Giup to aaaaa
=> MO là tia p/giác của góc AMB,OM là tia p/giác của góc AOB =>AMO=BMO=AMB/2=40/2=20
Vì AM là tiếp tuyến của đ.tròn (O)tại A =>tam giác AOM vuông tại A =>AMO+AOM=90=>AOM=90-20=70
Vậy góc AMO=20,góc AOM=70
b) Ta có OM là tia p/giác của góc AOB( câu a)=>AOB=2AOM=2x70=140
Vì AOB là góc ở tâm chắn cung AmB nên sđAmB=AOB=140
=>sđAnB=360-140=220