
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2x - 3 = x + 1/2
2x - x = 3 + 1/2 (chuyển x qua vế kia)
x = 7/2
Vậy x = 7/2


bài `2`
`a, x-1/2 =-3/4`
`=> x=-3/4 +1/2`
`=> x=-3/4 +2/4`
`=> x= -1/4`
`b, x+1/6 =-3/8`
`=> x=-3/8 - 1/6`
`=>x= -13/24`
`c, x-2/3 =3/5 -1/4`
`=> x-2/3 =7/20`
`=>x= 7/20 +2/3`
`=>x= 61/60`
`d, x-1/4 = 5/8 . 2/3`
`=> x-1/4 =5/12`
`=>x= 5/12 +1/4`
`=>x= 5/12 + 3/12`
`=>x= 2/3`
`e, 4/5 -x=-8/35`
`=>x= 4/5-(-8/35)`
`=>x= 4/5+8/35`
`=>x= 36/35`
`f, 11/12 x +3/4=1/6`
`=> 11/12 x =1/6-3/4`
`=> 11/12 x =-7/12`
`=>x=-7/12 : 11/12`
`=>x=-7/12 xx 12/11`
`=>x= -7/11`
`g, 2/9 - 2/7 x= 1/3`
`=> 2/7 x= 2/9- 1/3`
`=> 2/7 x=-1/9`
`=>x=-1/9 : 2/7`
`=>x=-1/9 xx 7/2`
`=>x= -7/18`
`h, x + (-7/15) = -1 1/20`
`=> x + (-7/15) =-21/20`
`=>x= -21/20 - (-7/15)`
`=>x= -21/20+7/15`
`=>x=-7/12`
`i, 3 1/5 x -7/10 = 1 3/5`
`=> 16/5 x -7/10 =8/5`
`=> 16/5 x =8/5 + 7/10`
`=> 16/5 x =23/10`
`=>x= 23/10 : 16/5`
`=>x= 23/10 xx 5/16`
`=>x= 23/32`
`b, x -1/2 = 3/4 : 3/2`
`=> x -1/2 = 3/4 xx 2/3`
`=> x -1/2 = 1/2`
`=>x= 1/2+1/2`
`=>x=1`
`k , 4/5 -1/2 x=1/10`
`=> 1/2 x=4/5 -1/10`
`=>1/2 x=7/10`
`=>x= 7/10 :1/2`
`=>x= 7/10 xx 2`
`=>x=7/5`


\(\frac{2}{1\times3}+\frac{2}{3\times5}+\frac{2}{5\times7}+...+\frac{2}{97\times99}+\frac{2}{99\times101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{97}-\frac{1}{99}+\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}\)
\(=\frac{100}{101}\)

Bài 1.
\(a,\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{4}{12}+\dfrac{3}{12}=\dfrac{7}{12}\)
\(b,\dfrac{-2}{5}+\dfrac{7}{21}=\dfrac{-42}{105}+\dfrac{35}{105}=\dfrac{-77}{105}=\dfrac{-11}{15}\)
\(c,\dfrac{3}{8}+\dfrac{-5}{6}=\dfrac{18}{48}+\dfrac{-40}{48}=\dfrac{-22}{48}=\dfrac{-11}{24}\)
\(d,\dfrac{-3}{4}+\dfrac{2}{5}=\dfrac{-15}{20}+\dfrac{8}{20}=\dfrac{-7}{20}\)
\(e,\dfrac{1}{6}+\dfrac{-3}{2}=\dfrac{2}{12}+\dfrac{-18}{12}=\dfrac{16}{12}=\dfrac{4}{3}\)
\(f,\dfrac{-2}{5}+\dfrac{-4}{3}=\dfrac{-6}{15}+\dfrac{-20}{15}=\dfrac{-26}{15}\)
\(g,\dfrac{1}{8}+\dfrac{-3}{4}=\dfrac{4}{32}+\dfrac{-24}{32}=\dfrac{20}{32}=\dfrac{5}{8}\)
\(h,\dfrac{-3}{4}+\dfrac{3}{7}=\dfrac{-21}{28}+\dfrac{12}{28}=\dfrac{-9}{28}\)
\(i,\dfrac{-3}{4}+\dfrac{-4}{5}=\dfrac{-15}{20}+\dfrac{-16}{20}=\dfrac{-31}{20}\)
\(k,\dfrac{-5}{25}+\dfrac{-7}{14}=\dfrac{-70}{350}+\dfrac{-175}{350}=\dfrac{-245}{350}=\dfrac{-7}{10}\)
\(l,\dfrac{6}{21}+\dfrac{-3}{15}=\dfrac{90}{315}+\dfrac{-63}{315}=\dfrac{27}{315}=\dfrac{3}{35}\)
\(m,\dfrac{3}{4}-\dfrac{5}{8}+\dfrac{1}{2}=\dfrac{24}{32}-\dfrac{20}{32}+\dfrac{1}{2}=\dfrac{4}{32}+\dfrac{1}{2}=\dfrac{1}{8}+\dfrac{1}{2}=\dfrac{2}{16}+\dfrac{8}{16}=\dfrac{10}{16}=\dfrac{5}{8}\)
\(n,\dfrac{-3}{12}-\dfrac{1}{-4}+\dfrac{-2}{6}=\dfrac{-1}{4}-\dfrac{1}{-4}+\dfrac{-1}{3}=0+\dfrac{-1}{3}=\dfrac{-1}{3}\)
\(p,\dfrac{1}{3}+\dfrac{-3}{4}-\dfrac{5}{12}=\dfrac{4}{12}+\dfrac{-9}{12}-\dfrac{5}{12}=\dfrac{-5}{12}-\dfrac{5}{12}=\dfrac{-10}{12}=\dfrac{-5}{6}\)
Bài 2:
\(a,\dfrac{3}{5}+x=\dfrac{5}{6}\)
\(x=\dfrac{5}{6}-\dfrac{3}{5}\)
\(x=\dfrac{7}{30}\)
\(b,x-\dfrac{1}{4}=\dfrac{-5}{8}\)
\(x=\dfrac{-5}{8}+\dfrac{1}{4}\)
\(x=\dfrac{-3}{8}\)
\(c,x-\dfrac{2}{3}=\dfrac{7}{12}\)
\(x=\dfrac{7}{12}+\dfrac{2}{3}\)
\(x=\dfrac{5}{4}\)
\(d,x+\dfrac{-7}{15}=-1\dfrac{1}{20}\)
\(x=-1\dfrac{1}{20}-\dfrac{-7}{15}\)
\(x=\dfrac{-7}{12}\)
\(e,x-\dfrac{1}{2}=\dfrac{-3}{4}\)
\(x=\dfrac{-3}{4}+\dfrac{1}{2}\)
\(x=\dfrac{-1}{4}\)
\(f,x-\dfrac{3}{4}=\dfrac{1}{2}\)
\(x=\dfrac{1}{2}+\dfrac{3}{4}\)
\(x=\dfrac{5}{4}\)
\(g,x-\dfrac{1}{4}=\dfrac{5}{8}\cdot\dfrac{2}{3}\)
\(x-\dfrac{1}{4}=\dfrac{5}{12}\)
\(x=\dfrac{5}{12}+\dfrac{1}{4}\)
\(x=\dfrac{2}{3}\)
\(h,\dfrac{4}{5}-x=\dfrac{-8}{35}\)
\(x=\dfrac{4}{5}-\dfrac{-8}{35}\)
\(x=\dfrac{36}{35}\)
#YVA

mún tính k/c đó phải có số đo cụ thể chứ . MA+NA=MN+1/2(a+b)

2: x+13 là bội của x-1
=>\(x+13⋮x-1\)
=>\(x-1+12⋮x-1\)
=>\(x-1\inƯ\left(12\right)\)
mà x-1>=-1(vì x là số tự nhiên)
nên \(x-1\in\left\{-1;1;2;3;4;6;12\right\}\)
=>\(x\in\left\{0;2;3;4;5;7;13\right\}\)
3: 4x+9 là bội của 2x+1
=>\(4x+9⋮2x+1\)
=>\(4x+2+7⋮2x+1\)
=>\(2x+1\in\left\{1;7\right\}\)
=>\(x\in\left\{0;3\right\}\)


 giúp mh vs ah
giúp mh vs ah

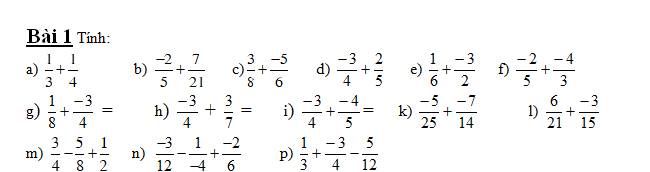
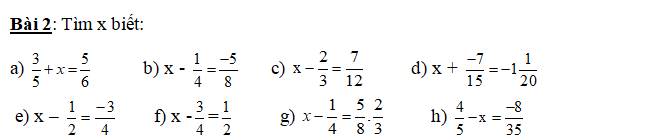

Bài 12:
a) \(\dfrac{12}{3n-1}\) là một số nguyên khi:
\(12\) ⋮ \(3n-1\)
\(\Rightarrow3n-1\inƯ\left(12\right)=\left\{1;-1;2;-2;3;-3;4;-4;6;-6;12;-12\right\}\)
\(\Rightarrow3n\in\left\{2;0;3;-1;4;-2;5;-3;7;-5;13;-11\right\}\)
\(\Rightarrow n\in\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};\dfrac{4}{3};-\dfrac{2}{3};\dfrac{5}{3};-1;\dfrac{7}{3};-\dfrac{5}{3};\dfrac{13}{3};-\dfrac{11}{3}\right\}\)
Mà: \(n\in Z\Rightarrow n\in\left\{0;1;-1\right\}\)
b) \(\dfrac{2n+3}{7}\) là một số nguyên khi:
\(2n+3\) ⋮ 7
\(\Rightarrow2n+3\in B\left(7\right)\)
Do \(n\in Z\) nên \(2n+3\) lẻ
\(\Rightarrow2n+3\in B\left(7,\text{lẻ}\right)\)
\(\Rightarrow n\in\dfrac{B\left(7,\text{lẻ}\right)-3}{2}\)
c) \(\dfrac{2n+5}{n-3}=\dfrac{2n-6+11}{n-3}=\dfrac{2\left(n-3\right)+11}{n-3}=2+\dfrac{11}{n-3}\)
Là một số nguyên khi:
11 ⋮ \(n-3\)
\(\Rightarrow n-3\inƯ\left(11\right)=\left\{1;-1;11;-11\right\}\)
\(\Rightarrow n\in\left\{4;2;14;-8\right\}\)
Bài 8:
S = \(\dfrac{3}{10}\) + \(\dfrac{3}{11}\) + \(\dfrac{3}{12}\) + \(\dfrac{3}{13}\) + \(\dfrac{3}{14}\)
\(\dfrac{3}{10}>\dfrac{3}{11}>\dfrac{3}{12}>\dfrac{3}{13}>\dfrac{3}{14}\)
S < \(\dfrac{3}{10}\).5 = \(\dfrac{3}{2}\) = 1 + \(\dfrac{1}{2}\)
S > \(\dfrac{3}{14}.5\) = \(\dfrac{15}{14}\) = 1 + \(\dfrac{1}{14}\)
Vì \(\dfrac{1}{14}\) < \(\dfrac{1}{2}\) nên
1 < \(\dfrac{15}{14}\) < S < \(\dfrac{3}{2}\) < 2
Vậy 1 < S < 2 (đpcm)