
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số sp mỗi ngày phân xưởng đó sản xuất được theo dự định là a (sản phẩm) (a: nguyên, dương)
Vậy số ngày sản xuất dự kiến là: 1100/a (ngày)
Vì vượt mức 5sp/1 ngày nên số ngày sản xuất thực tế là: 1100/(a+5) (ngày)
Vì phân xưởng làm hoàn thành sớm hơn 2 ngày, nên ta có pt:
\(\dfrac{1100}{a}=\dfrac{1100}{a+5}+2\left(a\ne0;a\ne-5\right)\\ \Leftrightarrow\dfrac{1100\left(a+5\right)}{a\left(a+5\right)}=\dfrac{1100a+2a\left(a+5\right)}{a\left(a+5\right)}\\ \Leftrightarrow2a^2+10a-5500=0\\ \Leftrightarrow2a^2-100a+110a-5500=0\\ \Leftrightarrow2a\left(a-50\right)+110\left(a-50\right)=0\\ \Leftrightarrow\left(2a+110\right)\left(a-50\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2a+110=0\\a-50=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-55\left(loại\right)\\a=50\left(Nhận\right)\end{matrix}\right.\)
Vậy theo kế hoạch, mỗi ngày phân xưởng phải sx được 50 sản phẩm


1: Khi x=25 thì A=(2*5)/(5+2)=10/7
2: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{x-4}=\dfrac{2\left(\sqrt{x}-2\right)}{x-4}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
3: căn x+2>=2
=>P<=2/2=1
Dấu = xảy ra khi x=0

Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi



1: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>CE\(\perp\)AB tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
=>BD\(\perp\)AC tại D
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại F
2: Xét ΔFBH vuông tại F và ΔFAC vuông tại F có
\(\widehat{FBH}=\widehat{FAC}\left(=90^0-\widehat{ACF}\right)\)
Do đó: ΔFBH~ΔFAC
=>\(\dfrac{FB}{FA}=\dfrac{FH}{FC}\)
=>\(FB\cdot FC=FA\cdot FH\)
3: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=90^0+90^0=180^0\)
nên AEHD là tứ giác nội tiếp đường tròn đường kính AH
Tâm I là trung điểm của AH


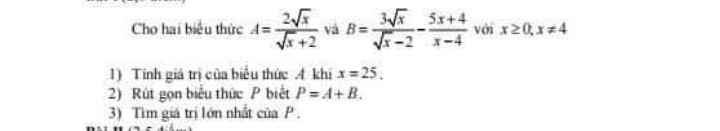




Thank