
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$

\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)


c: \(\dfrac{x}{5}=-\dfrac{3}{2}\)
nên \(x=-\dfrac{15}{2}\)

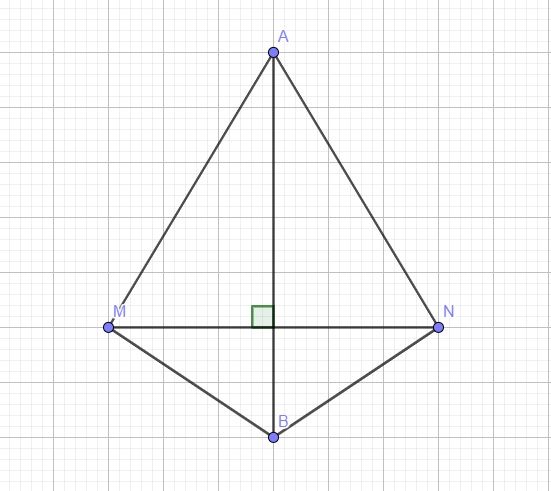
Do A thuộc trung trực đoạn MN nên \(AM=AN\)
Do B thuộc trung trực đoạn MN nên \(BM=BN\)
Xét 2 tam giác MAB và NAB có:
\(\left\{{}\begin{matrix}AM=AN\left(cmt\right)\\BM=BN\left(cmt\right)\\AB\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta MAB=\Delta NAB\left(c.c.c\right)\)

Bài 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}=\dfrac{a+b+c}{9+7+8}=\dfrac{120}{24}=5\)
Do đó: a=45; b=35; c=40



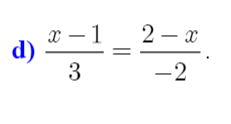

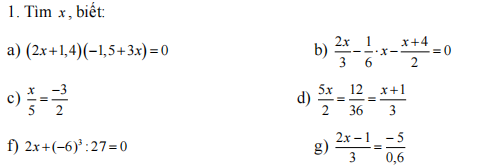




\(a,\left(152\frac{1}{2}-148\frac{3}{8}\right):0,2=x:0,3\)
\(\left(\frac{305}{2}-\frac{1187}{8}\right):\frac{2}{10}=x:\frac{3}{10}\)
\(\left(\frac{1220}{8}-\frac{1187}{8}\right):\frac{1}{5}=x\times\frac{10}{3}\)
\(\frac{33}{8}\times5=\frac{10x}{3}\)
\(\frac{165}{8}=\frac{10x}{3}\)
\(\Leftrightarrow8.10x=165.3\)
\(80x=495\)
\(x=495:80\)
\(x=\frac{99}{16}\)
b, tương tự ý a
\(c,\frac{x-1}{x+5}=\frac{6}{7}\)
\(\Leftrightarrow7\left(x-1\right)=6\left(x+5\right)\)
\(7x-7=6x+30\)
\(\Rightarrow7x-7-6x-30=0\)
\(x-37=0\)
\(x=37\)