
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
a. Vì hệ số góc $2>0$ nên hàm số đồng biến trên $R$
b. Đồ thị $y=2x-3$ như sau:
c. Để hai đt đã cho cắt nhau thì $2\neq m+1$
$\Leftrightarrow m\neq 1$
Vạy $m\neq \pm 1$ để 2 đt cắt nhau.

Áp dụng hệ thức lượng:
\(AH^2=BH.CH=4.9=36\)
\(\Rightarrow AH=6\left(cm\right)\)
\(BC=4+9=13\left(cm\right)\)
- Nếu \(BH=4\)
Áp dụng hệ thức lượng:
\(AB^2=BH.BC\Rightarrow AB=\sqrt{4.13}=2\sqrt{13}\) (cm)
\(sinC=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{13}\Rightarrow C\approx33^041'\)
- Nếu \(BH=9\Rightarrow AB=\sqrt{BH.BC}=\sqrt{9.13}=3\sqrt{13}\left(cm\right)\)
\(sinC=\dfrac{AB}{BC}=\dfrac{3\sqrt{13}}{13}\Rightarrow C\approx56^019'\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.6.13=39\left(cm^2\right)\)
(Vì đề không nói rõ BH, CH bằng 4 hay 9 nên mình cho BH = 4 và CH = 9 nhé!)
Áp dụng HTL vào \(\Delta ABC\) vuông tại A đường cao AH:
\(AH^2=BH\cdot HC\Leftrightarrow AH=\sqrt{BH\cdot HC}=\sqrt{4\cdot9}=6\left(cm\right)\)
Áp dụng HTL vào \(\Delta ABH\) vuông tại H:
\(AB^2=AH^2+BH^2\Leftrightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
Áp dụng tslg vào \(\Delta ABC\) vuông tại A, đường cao AH:
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{2\sqrt{13}}{4+9}\approx34^0\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot2\sqrt{13}\cdot\left(\sqrt{13^2-\left(2\sqrt{13}\right)^2}\right)_{Pytago}=39cm^2\)




ĐẶT x-1=a , x+3=b (a,b cùng dấu)
\(PT\Leftrightarrow ab+2a\sqrt{\frac{b}{a}}=8\)
\(\Leftrightarrow2a\sqrt{\frac{b}{a}}=8-ab\)
\(\Leftrightarrow4a^2\frac{b}{a}=64-16ab+a^2b^2\)
\(\Leftrightarrow a^2b^2-20ab+64=0\)
\(\Leftrightarrow\left(ab-10\right)^2-36=0\)
\(\Leftrightarrow\left(ab-4\right)\left(ab-16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}ab=4\\ab=16\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x-1\right)\left(x+3\right)=4\\\left(x-1\right)\left(x+3\right)=16\end{cases}}\)
Đến đây đơn giản rồi bn tự giải nhé
ĐK:....\(\frac{x+3}{x-1}\ge0\)
<=> \(\left(x-1\right)\left(x+3\right)+2\sqrt{\left(x-1\right)\left(x+3\right)}+1=9\)
<=> \(\left(\sqrt{\left(x-1\right)\left(x+3\right)}+1\right)^2=9\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{\left(x-1\right)\left(x+3\right)}=2\\\sqrt{\left(x-1\right)\left(x+3\right)}=-4\left(loai\right)\end{cases}}\)
\(\Leftrightarrow\left(x-1\right)\left(x+3\right)=4\)
Em tự làm tiếp nhé
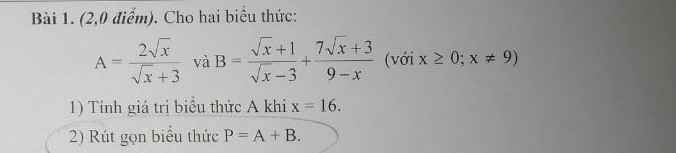







1: Thay x=16 vào A, ta được:
\(A=\dfrac{2\cdot4}{4+3}=\dfrac{8}{7}\)