
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)

Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

\(\left|3x+2\right|=\left|4x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=4x-3\\3x+2=3-4x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-x=-5\\7x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{7}\end{matrix}\right.\)
\(\left|2+3x\right|=\left|4x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2+3x=4x-3\\2+3x=3-4x\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{7}\end{matrix}\right.\)

\(P\left(0\right)=a\cdot0^3+b\cdot0^3+c\cdot0+d=2017\)
\(\Leftrightarrow d=2017\)
\(P\left(1\right)=a\cdot1^3+b\cdot1^2+c\cdot1+d=2\)
\(\Leftrightarrow a+b+a+d=2\)
\(P\left(-1\right)=a\cdot\left(-1\right)^3+b\cdot\left(-1\right)^2+c\cdot\left(-1\right)+d=6\)
\(\Leftrightarrow-a+b-c+d=6\)
\(P\left(2\right)=a\cdot2^3+b\cdot2^2+c\cdot2+d=-6033\)
\(\Leftrightarrow8a+4b+2c+d=-6033\)

 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU
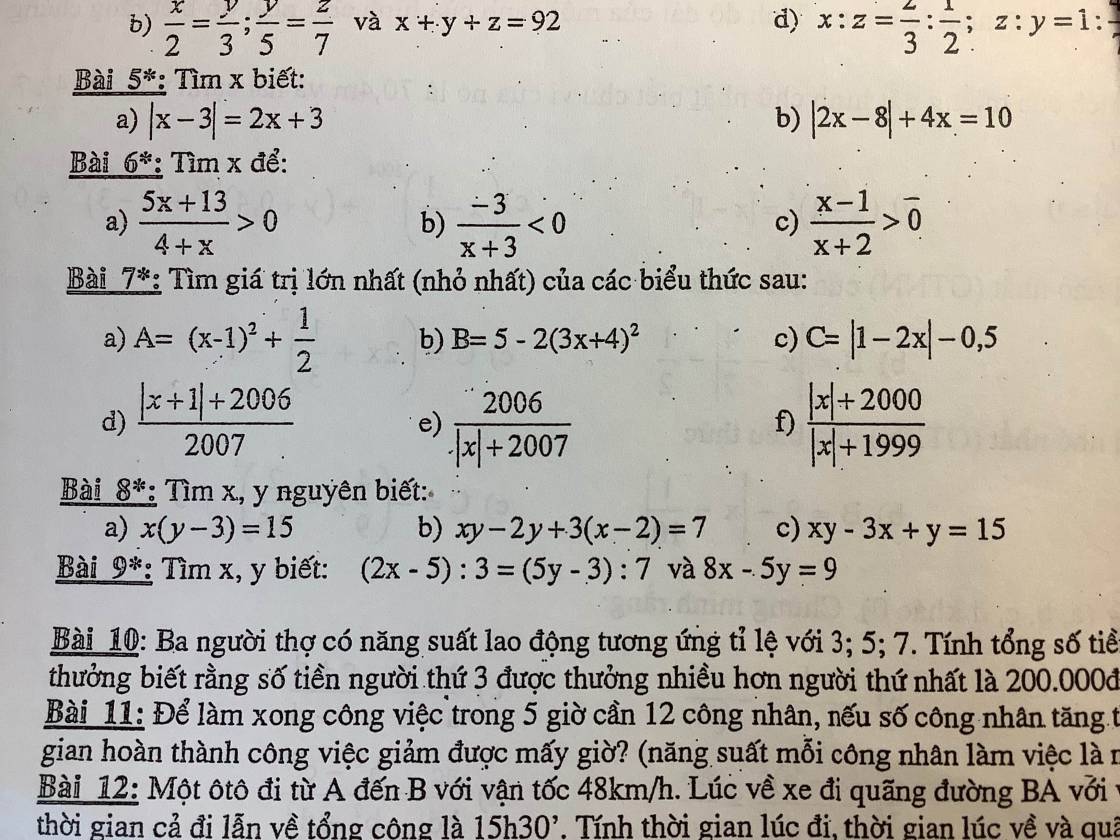

 GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!
GIÚP MÌNH VỚI Ạ MÌNH ĐANG CẦN GẤP Ạ MINH CẢM ƠN RẤT NHIỀU!!!!