
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
hay CD\(\perp\)AC
2: Xét ΔCAE có
CH là đường cao
CH là đường trung tuyến
DO đó: ΔCAE cân tại C
3: Ta có: ABDC là hình bình hành
nên CA=BD
mà CA=CE
nên BD=CE

Hướng dẫn giải:
Do I thuộc đường trung trực của BC nên BI=CI
Ta có:△AHI=△AKI(cạnh huyền- góc nhọn)
\(\Rightarrow HI=KI\)
\(\Rightarrow\text{△BHI}\)\(=\text{△CKI}\)(cạnh huyền- cạnh góc vuông)
\(\Rightarrow BH=CK\)

1: Xét ΔAEB và ΔCED có
EA=EC
EB=ED
AB=CD
=>ΔAEB=ΔCED
2: ΔAEB=ΔCED
=>góc BAE=góc DCE
=>góc BAE=góc CAE
=>AE là phân giác của góc BAC

1:
a: Xét ΔBCD vuông tại B và ΔKCD vuông tại K có
CD chung
\(\widehat{BCD}=\widehat{KCD}\)
Do đó: ΔBCD=ΔKCD
Suy ra: BC=KC
=>ΔBKC cân tại C
mà \(\widehat{BCK}=60^0\)
nên ΔBKC đều
b: Ta có: BC=KC
nên C nằm trên đường trung trực của BK(1)
Ta có: DB=DK
nên D nằm trên đường trung trực của BK(2)
Từ (1) và (2) suy ra DC là đường trung trực của BK

\(a,x=\dfrac{1}{2};y=-100\)
\(\Rightarrow A=\dfrac{1}{2}\left[\left(\dfrac{1}{2}\right)^2+100\right]-\left(\dfrac{1}{2}\right)^2\left(\dfrac{1}{2}-100\right)-100\left[\left(\dfrac{1}{2}\right)^2-\dfrac{1}{2}\right]\)
\(\Rightarrow A=100\)
\(b,x=-1\)
\(\Rightarrow B=\left[\left(-1\right)^2-5\right]\left(-1+3\right)+\left(-1+4\right)\left[-1-\left(-1\right)^2\right]\)
\(\Rightarrow B=-14\)
\(c,x=-2\)
\(\Rightarrow C=-6\left(5.4-2\right)-5.4\left(7-6\right)-2,5\left(2-14.4\right)\)
\(\Rightarrow C=7\)
\(d,\left|x\right|=2\)
\(TH_1:x\ge0\)
\(D=\left(3.2+5\right)\left(2.2-1\right)+\left(4.2-1\right)\left(3.2+2\right)=89\)
\(TH_2:x< 0\)
\(D=\left(-6+5\right)\left(-4-1\right)+\left(-8-1\right)\left(-6+2\right)=41\)
 giúp mình với mình tick cho
giúp mình với mình tick cho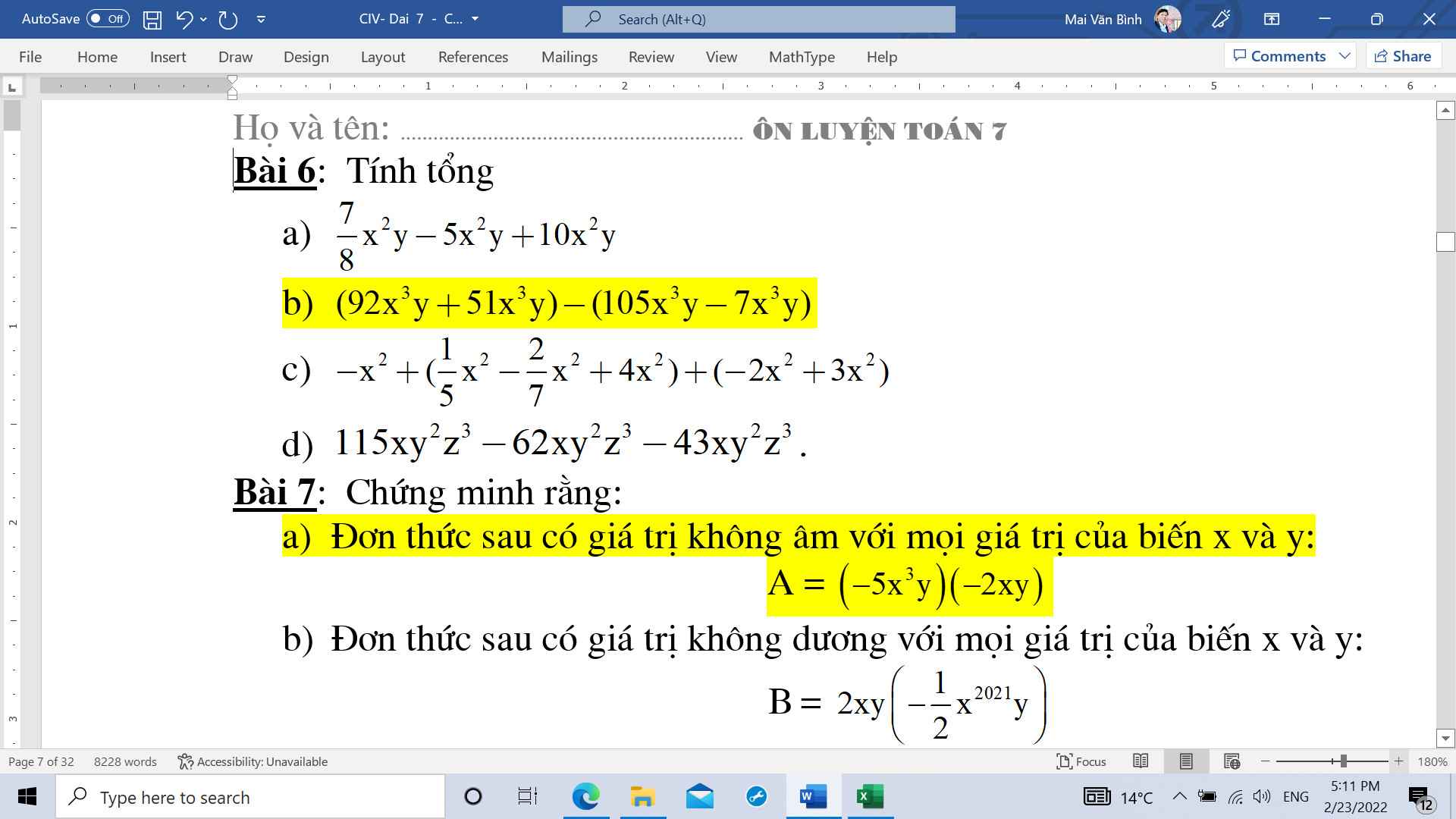
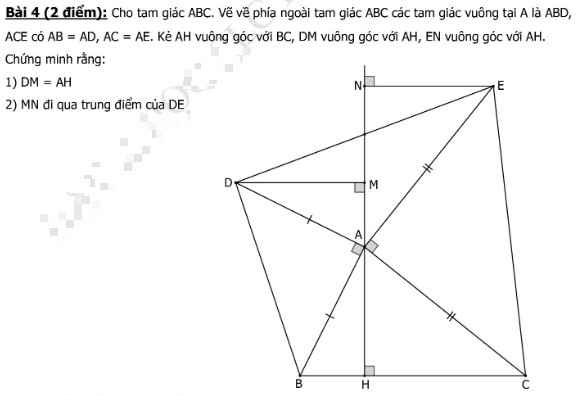 Giúp mình với mình tick cho !
Giúp mình với mình tick cho ! Giúp mình với mình tick cho .
Giúp mình với mình tick cho .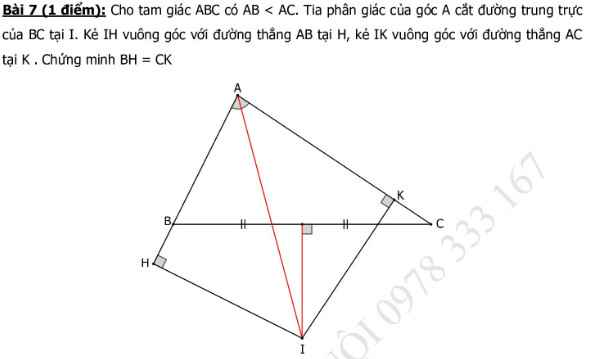


 Làm giúp mình với, mình sẽ tick cho mng
Làm giúp mình với, mình sẽ tick cho mng Giúp mình làm bài này với , mình tick cho .
Giúp mình làm bài này với , mình tick cho .
1:
a:
Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b:Ta có: ΔABD=ΔEBD
nên BA=BE
hay ΔBAE cân tại B
c: Ta có: ΔABD=ΔEBD
nên DA=DE
hay ΔDAE cân tại D
2:
a: Ta có:AH⊥BC
DE⊥BC
Do đó: AH//DE