
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 4:
1: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=\left(20a\right)^2+\left(21a\right)^2=841a^2\)
=>\(BC=\sqrt{841a^2}=29a\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\)
=>\(BH\cdot29a=\left(20a\right)^2=400a^2\)
=>\(BH=\dfrac{400}{29}a\)
2: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Xét ΔMAB có MA=MB
nên ΔMAB cân tại M
=>\(tanBAM=tanABM=tanABC=\dfrac{AC}{AB}=\dfrac{21}{20}\)
Câu 5:
1: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>BD\(\perp\)DA tại D
=>BD\(\perp\)AC tại D
Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
=>AE\(\perp\)EB tại E
=>AE\(\perp\)BC tại E
Xét ΔCAB có
AE,BD là các đường cao
AE cắt BD tại H
Do đó: H là trực tâm của ΔCAB
=>CH\(\perp\)AB
2:
Gọi giao điểm của CH với AB là K
=>CH\(\perp\)AB tại K
Ta có: ΔCDH vuông tại D
mà DF là đường trung tuyến
nên FH=FD=FC
\(\widehat{FDO}=\widehat{FDH}+\widehat{ODB}\)
\(=\widehat{OBD}+\widehat{FHD}\)
\(=\widehat{KHB}+\widehat{KBH}=90^0\)
=>FD\(\perp\)DO tại D
=>FD là tiếp tuyến của (O)

e: \(\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\cdot\sqrt{ab}\)
\(=a\cdot\sqrt{\dfrac{a}{b}\cdot\sqrt{ab}+2ab}+b\cdot\sqrt{\dfrac{a}{b}\cdot ab}\)
\(=a\cdot\sqrt{\dfrac{a\sqrt{ab}+2ab^2}{b}}+b\cdot a\)
\(=a\left(\sqrt{\dfrac{a\sqrt{ab}+2ab^2}{b}}+b\right)\)
\(=a\left(\dfrac{\sqrt{ab\sqrt{ab}+2ab^3}+b^2}{b}\right)\)

6:
a: Xét ΔABH vuông tại H có \(cosB=\dfrac{BH}{AB}\)
=>\(cosB=\dfrac{4}{16}=\dfrac{1}{4}\)
Xét ΔABC vuông tại A có \(cosB=\dfrac{BA}{BC}\)
=>\(\dfrac{16}{BC}=\dfrac{1}{4}\)
=>BC=64(cm)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=64^2-16^2=3840\)
=>\(AC=\sqrt{3840}=16\sqrt{15}\left(cm\right)\)
b: Xét ΔABN vuông tại A có AD là đường cao
nên \(BN\cdot BD=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BN\cdot BD=BH\cdot BC\)


\(\sqrt{2-\sqrt{3}}=\frac{\sqrt{2}\sqrt{2-\sqrt{3}}}{\sqrt{2}}=\frac{\sqrt{2.\left(2-\sqrt{3}\right)}}{\sqrt{2}}=\frac{\sqrt{4-2\sqrt{3}}}{\sqrt{2}}\)
\(=\frac{\sqrt{3-2\sqrt{3}.1+1}}{\sqrt{2}}=\frac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}=\frac{\sqrt{3}-1}{\sqrt{2}}=\frac{\sqrt{2}\sqrt{3}-\sqrt{2}}{2}\)
\(=\frac{\sqrt{6}-\sqrt{2}}{2}\)

Câu 3:
a: A=1/2
=>\(\dfrac{\sqrt{x}-2}{\sqrt{x}}=\dfrac{1}{2}\)
=>\(2\sqrt{x}-4=\sqrt{x}\)
=>\(2\sqrt{x}-\sqrt{x}=4\)
=>\(\sqrt{x}=4\)
=>x=16(nhận)
b: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{x-1}\)
\(=\dfrac{\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-2\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
\(\sqrt{P}< \dfrac{1}{2}\)
=>\(0< =P< \dfrac{1}{4}\)
=>P>=0 và P<1/4
=>P>=0 và P-1/4<0
=>\(\left\{{}\begin{matrix}\dfrac{\sqrt{x}-2}{\sqrt{x}+1}>=0\\\dfrac{\sqrt{x}-2}{\sqrt{x}+1}-\dfrac{1}{4}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}-2>=0\\\dfrac{4\sqrt{x}-8-\sqrt{x}-1}{4\left(\sqrt{x}+1\right)}< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{x}>=2\\3\sqrt{x}-9< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}>=2\\\sqrt{x}< 3\end{matrix}\right.\)
=>\(2< =\sqrt{x}< 3\)
=>4<=x<9
 Giúp tớ câu 3 với aaa:<
Giúp tớ câu 3 với aaa:< Giúp tớ câu 4 hoặc câu 5 với ạ
Giúp tớ câu 4 hoặc câu 5 với ạ

 giúp e gấp với aaa
giúp e gấp với aaa
 giúp e với aaa, e cảm ơn
giúp e với aaa, e cảm ơn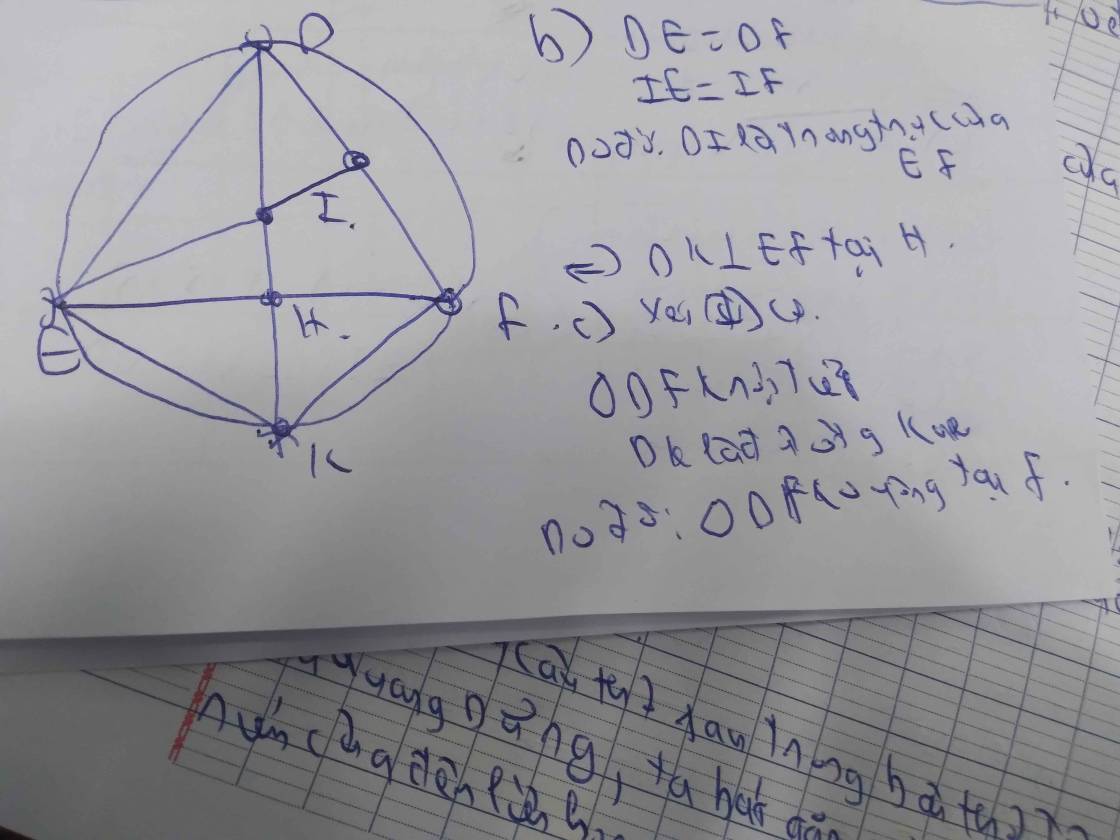

Câu 3:
a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Ta có: OC là phân giác của góc MOA
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
=>\(AC\cdot BD=OM^2=R^2\)
c: Ta có:AC\(\perp\)AB
BD\(\perp\)AB
Do đó: AC//BD
Xét ΔNCA và ΔNBD có
\(\widehat{NCA}=\widehat{NBD}\)(hai góc so le trong, AC//BD)
\(\widehat{CNA}=\widehat{BND}\)(hai góc đối đỉnh)
Do đó: ΔNCA đồng dạng với ΔNBD
=>\(\dfrac{NC}{NB}=\dfrac{AC}{BD}=\dfrac{NA}{ND}\)
=>\(\dfrac{NA}{ND}=\dfrac{MC}{MD}\)
=>\(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
Xét ΔDAC có \(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
nên MN//AC