
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(1\dfrac{2}{3}-\left(\dfrac{1}{2}x-0,75\right)=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{5}{3}-\dfrac{1}{2}x+\dfrac{3}{4}=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{29}{12}-\dfrac{1}{2}x=-\dfrac{1}{6}\)
\(\Rightarrow\dfrac{1}{2}x=\dfrac{29}{12}+\dfrac{1}{6}\)
\(\Rightarrow\dfrac{1}{2}x=\dfrac{31}{12}\)
\(\Rightarrow x=\dfrac{31}{12}:\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{31}{6}\)
c) \(\left(x-1\dfrac{1}{2}\right)-\dfrac{3}{12}=\left(-\dfrac{1}{2}\right)^2\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)-\dfrac{3}{12}=\dfrac{1}{4}\)
\(\Rightarrow x-\dfrac{7}{4}=\dfrac{1}{4}\)
\(\Rightarrow x=\dfrac{1}{4}+\dfrac{7}{4}\)
\(\Rightarrow x=\dfrac{8}{4}\)
\(\Rightarrow x=2\)

Ta có \(\frac{2x}{3y}=-\frac{1}{3}\)
\(\Leftrightarrow\frac{2x}{-1}=\frac{3y}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{2x}{-1}=\frac{3y}{3}=\frac{2x+3y}{-1+3}=\frac{7}{2}\)
\(\Rightarrow\hept{\begin{cases}\frac{2x}{-1}=\frac{7}{2}\\\frac{3y}{3}=\frac{7}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x=-\frac{7}{2}\\y=\frac{7}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-\frac{7}{4}\\y=\frac{7}{2}\end{cases}}\)
Vậy \(x=-\frac{7}{4};y=\frac{7}{2}\)
K chắc
Học tốt
## Mirai
Theo bài ra ta cs
\(\frac{2x}{3y}=-\frac{1}{3}\Rightarrow\frac{2x}{-1}=\frac{3y}{3}\)và \(2x+3y=7\)
ADTC dãy tỉ số bằng nhau ta cs
\(\frac{2x}{-1}=\frac{3y}{3}=\frac{2x+3y}{-1+3}=\frac{7}{2}\)
\(\Rightarrow\hept{\begin{cases}\frac{2x}{-1}=\frac{7}{2}\\\frac{3y}{3}=\frac{7}{2}\end{cases}\Rightarrow\hept{\begin{cases}2x=-\frac{7}{2}\\3y=\frac{21}{2}\end{cases}\Rightarrow}\hept{\begin{cases}x=-\frac{7}{4}\\y=\frac{7}{2}\end{cases}}}\)

*Kẻ By’ là tia đối của tia By => ABy kề bù với ABy’
=> ABy + ABy’ = 180
=> 120 + ABy’ = 180
=> ABy’ = 60
Ta có mAx = 60 =ABy’ , mà mAx và ABy’ ở vị trí đồng vị => Ax // By (1)
*Ta có yBC + CBA + ABy = 360
=> yBC + 90 + 120 = 360
=> yBC = 150
Ta có BCz = 150 = yBC, mà 2 góc này ở vị trí so le trong => By // Cz (2)
Từ (1), (2) => đpcm


Lời giải:
ĐKĐB $\Rightarrow \frac{2}{c}=\frac{a+b}{ab}\Rightarrow c(a+b)=2ab$
Khi đó:
$\frac{a}{b}-\frac{a-c}{c-b}=\frac{a(c-b)-b(a-c)}{b(c-b)}=\frac{ac-ab-ab+bc}{b(c-b)}=\frac{c(a+b)-2ab}{b(c-b)}=\frac{2ab-2ab}{b(c-b)}=0$
$\Rightarrow \frac{a}{b}=\frac{a-c}{c-b}$ (đpcm)

a: Ta có: \(\left(\dfrac{3}{5}-\dfrac{7}{4}\right):\dfrac{23}{10}\)
\(=\dfrac{12-35}{20}\cdot\dfrac{10}{23}\)
\(=\dfrac{-23\cdot10}{23\cdot20}=-\dfrac{1}{2}\)
b: Ta có: \(\left(-\dfrac{2}{3}+\dfrac{3}{4}\right)^2\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{144}\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{60}-\dfrac{11}{5}=\dfrac{1}{60}-\dfrac{132}{60}=\dfrac{-131}{60}\)

Lời giải:
Nếu $x+y+z=0$ thì:
$\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}=0$
$\Rightarrow x=y=z=0$ (thỏa mãn)
Nếu $x+y+z\neq 0$ thì áp dụng tính chất dãy tỉ số bằng nhau:
$x+y+z=\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}=\frac{x+y+z}{y+z+1+x+z+2+x+y-3}=\frac{x+y+z}{2(x+y+z)}=\frac{1}{2}$
Khi đó:
Từ điều kiện $\frac{x}{y+z+1}=\frac{y}{x+z+2}=\frac{z}{x+y-3}$
$\Rightarrow \frac{x}{x+y+z+1}=\frac{y}{x+y+z+2}=\frac{z}{x+y+z-3}$
$\Leftrightarrow \frac{x}{\frac{3}{2}}=\frac{y}{\frac{5}{2}}=\frac{z}{\frac{-5}{2}}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{\frac{3}{2}}=\frac{y}{\frac{5}{2}}=\frac{z}{\frac{-5}{2}}=\frac{x+y+z}{\frac{3}{2}+\frac{5}{2}+\frac{-5}{2}}=\frac{\frac{1}{2}}{\frac{3}{2}}=\frac{1}{3}$
$\Rightarrow x=\frac{1}{2}; y=\frac{5}{6}; z=\frac{-5}{6}$
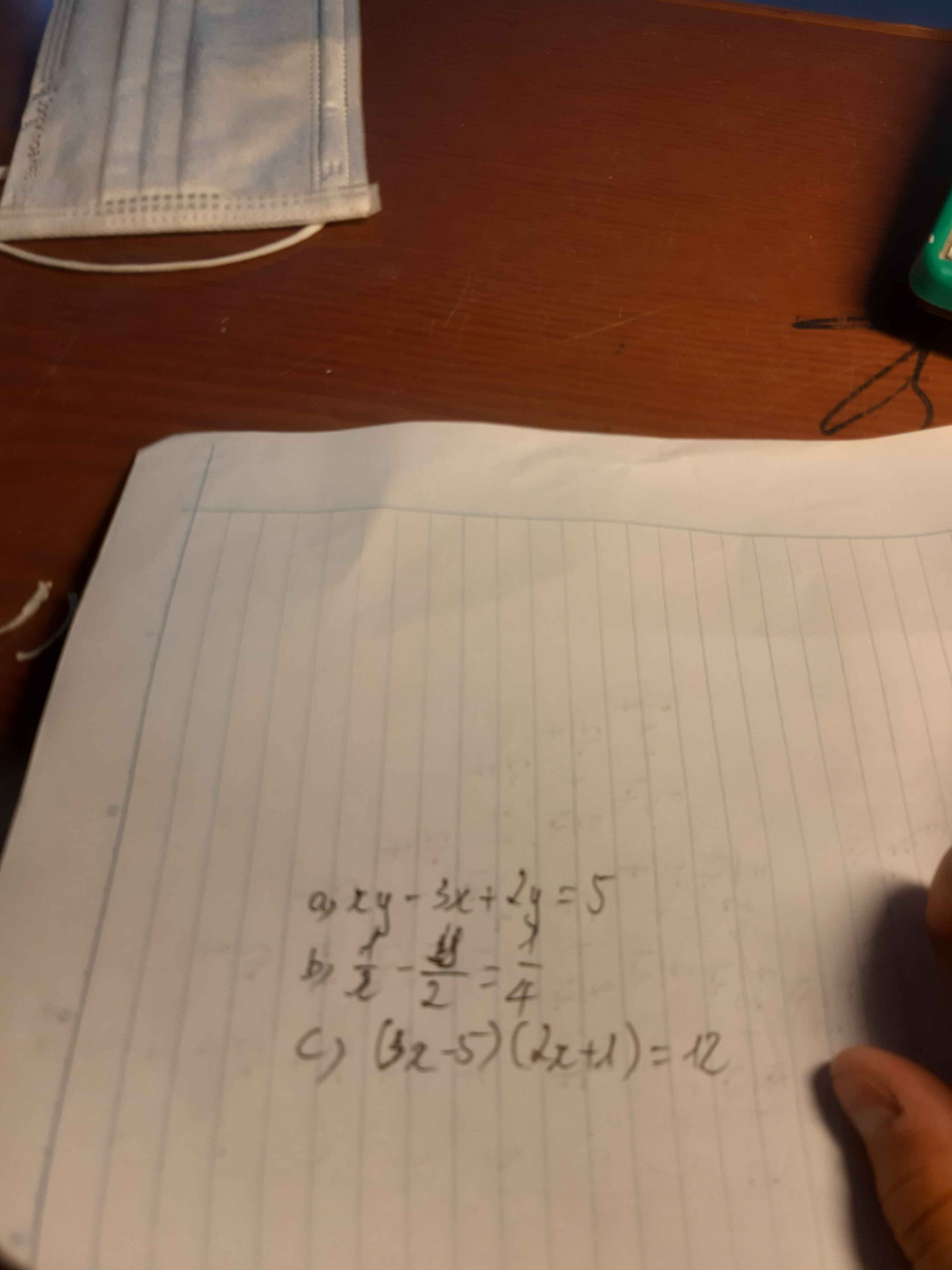
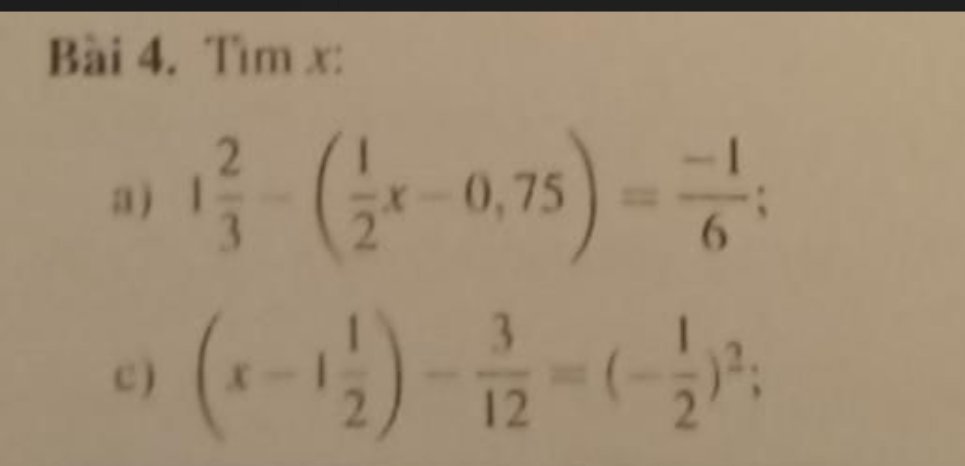



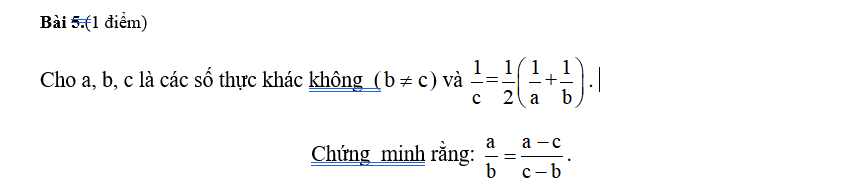


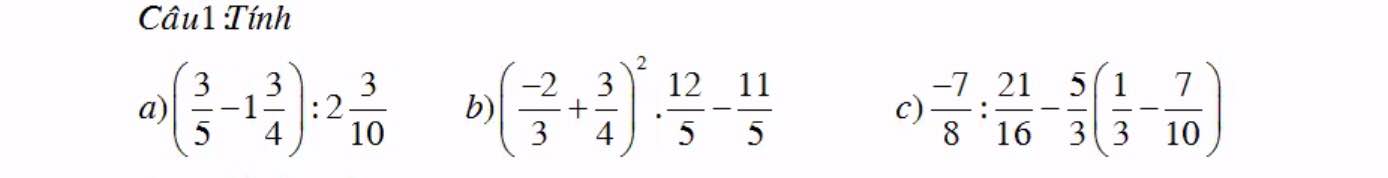
c) Ta có: \(\left(3x-5\right)\left(2x+1\right)=12\)
\(\Leftrightarrow6x^2+3x-10x-5-12=0\)
\(\Leftrightarrow6x^2-7x-17=0\)
\(\Delta=\left(-7\right)^2-4\cdot6\cdot\left(-17\right)=49+408=457\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{7+\sqrt{457}}{12}\\x_2=\dfrac{7-\sqrt{457}}{12}\end{matrix}\right.\)
Giải thường chứ đừng giải phương trình