Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)

Điều kiện : x, y > 12, x,y ∈ N.

Một ngày đội I làm được :  (công việc).

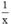Một ngày đội II làm được :  (công việc).

+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: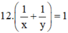 

+ Hai đội cùng làm trong 8 ngày được: 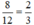 công việc.

⇒ còn lại đội II phải hoàn thành một mình 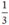 công việc.

Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được 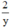 công việc.

Đội II hoàn thành 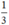 công việc còn lại trong 3,5 ngày nên ta có phương trình: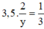 

Ta có hệ phương trình:

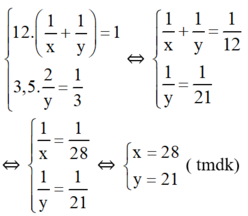
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Gọi thời gian đội I và đội II làm một mình xong công việc lần lượt là x; y (ngày)

Điều kiện : x, y > 12, x,y ∈ N.

Một ngày đội I làm được : 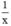 (công việc).

Một ngày đội II làm được :  (công việc).

+ Hai đội cùng làm sẽ xong trong 12 ngày nên ta có phương trình: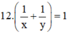 

+ Hai đội cùng làm trong 8 ngày được: 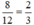 công việc.

⇒ còn lại đội II phải hoàn thành một mình 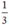 công việc.

Vì đội II tăng năng suất gấp đôi nên một ngày đội II làm được 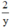 công việc.

Đội II hoàn thành 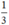 công việc còn lại trong 3,5 ngày nên ta có phương trình: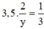 

Ta có hệ phương trình:

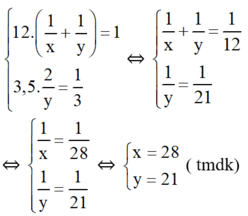
Vậy nếu làm một mình, đội I làm xong công việc trong 28 ngày, đội II làm xong công việc trong 21 ngày.

Gọi thời gian làm riêng xong việc của tổ 1 là x>0 (giờ) và tổ 2 là y>0 giờ

Trong 1 giờ hai tổ lần lượt làm được \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần công việc

Do 2 tổ làm chung trong 8 giờ thì hoàn thành nên: \(8\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)

Hai đội làm việc chung trong 6h và đội 1 làm việc 1 mình thêm 6h thì hoàn thành nên:

\(6\left(\dfrac{1}{x}+\dfrac{1}{y}\right)+6.\dfrac{1}{x}=1\) \(\Leftrightarrow\dfrac{2}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)

Ta được hệ pt: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\\\dfrac{2}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\)  \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=24\\y=12\end{matrix}\right.\)

Gọi x(h) là thời gian tổ 1 hoàn thành công việc khi làm một mình

y(h) là thời gian tổ 2 hoàn thành công việc khi làm một mình

(Điều kiện: x>6; y>6)

Trong 1 giờ, tổ 1 làm được: \(\dfrac{1}{x}\)(công việc)

Trong 1 giờ, tổ 2 làm được: \(\dfrac{1}{y}\)(công việc)

Trong 1 giờ, hai tổ làm được: \(\dfrac{1}{6}\)(công việc)

Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)

Trong 12 giờ, tổ 1 làm được: \(\dfrac{12}{x}\)(công việc)

Trong 2 giờ, tổ 2 làm được: \(\dfrac{2}{y}\)(công việc)

Theo đề, ta có phương trình: \(\dfrac{12}{x}+\dfrac{2}{y}=1\)(2)

Từ (1) và (2) ta lập được hệ phương trình:

\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{12}{x}+\dfrac{2}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{12}{x}+\dfrac{12}{y}=2\\\dfrac{12}{x}+\dfrac{2}{y}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10}{y}=1\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=10\\\dfrac{1}{x}+\dfrac{1}{10}=\dfrac{1}{6}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{15}\\y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=15\\y=10\end{matrix}\right.\)(thỏa ĐK)

Vậy: Tổ 1 cần 15 giờ để hoàn thành công việc khi làm một mình

Tổ 2 cần 10 giờ để hoàn thành công việc khi làm một mình

em đéo biết