a) \(y =  - {x^2} + 6x - 9\)

Ta có: \(a =  - 1\) nên parabol quay bề lõm xuống dưới.

Đỉnh \(I\left( {3;0} \right).\) Trục đối xứng \(x = 3.\) Giao điểm của đồ thị với trục \(Oy\) là: \(A\left( {0; - 9} \right).\) Parabol cắt trục hoành tại \(x = 3.\)

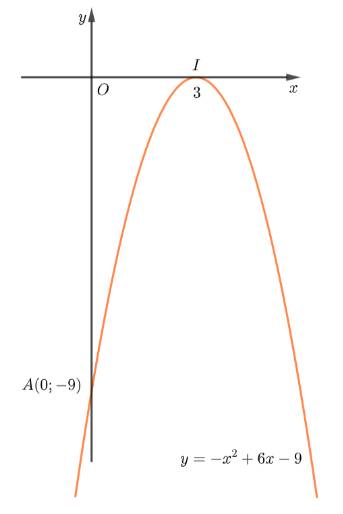
Tập giá trị của hàm số là: \(\left( { - \infty ;0} \right].\)

Từ đồ thị ta thấy: Hàm số \(y =  - {x^2} + 6x - 9\) đồng biến trên khoảng \(\left( { - \infty ;3} \right)\) và nghịch biến trên khoảng \(\left( {3; + \infty } \right).\)

b) \(y =  - {x^2} - 4x + 1\)

Ta có: \(a =  - 1\) nên parabol quay bề lõm xuống dưới.

Đỉnh \(I\left( { - 2;5} \right).\) Trục đối xứng \(x =  - 2.\) Giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;1} \right).\) Giao điểm của hàm số với trục \(Ox\) là: \(x =  - 2 + \sqrt 5 \) và \(x =  - 2 - \sqrt 5 .\)

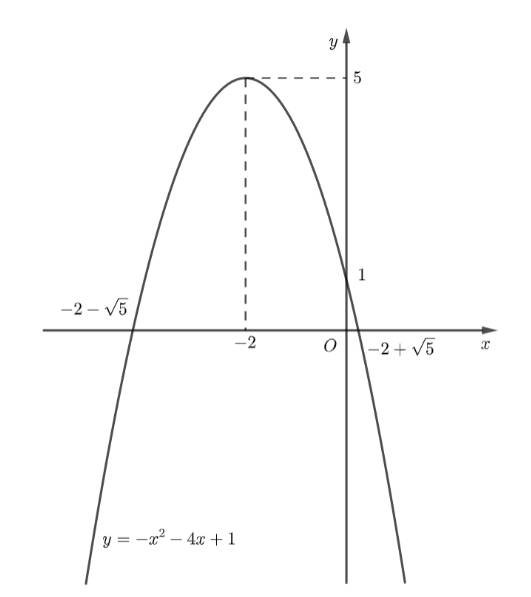
Tập giá trị của hàm số là: \(\left( { - \infty ;5} \right].\)

Từ đồ thị ta thấy: Hàm số \(y =  - {x^2} - 4x + 1\) đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\) và nghịch biến trên khoảng \(\left( { - 2; + \infty } \right).\)

c) \(y = {x^2} + 4x\)

Ta có: \(a = 1 > 0\) nên parabol quay bề lõm lên trên.

Đỉnh \(I\left( { - 2; - 4} \right).\) Trục đối xứng \(x =  - 2.\) Giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;0} \right).\) Giao điểm của hàm số với trục \(Ox\) là: \(x = 0\) và \(x =  - 4.\)

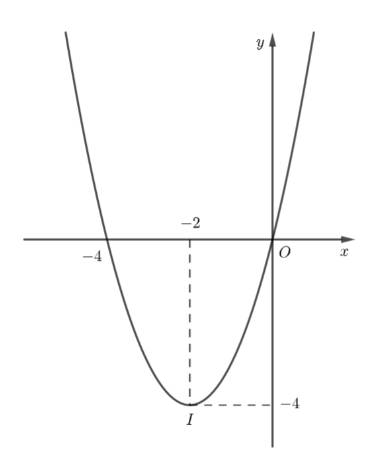
Tập giá trị của hàm số là: \(\left[ { - 4; + \infty } \right).\)

Từ đồ thị ta thấy: Hàm số \(y = {x^2} + 4x\) đồng biến trên khoảng \(\left( { - 2; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - 2} \right).\)

d) \(y = 2{x^2} + 2x + 1\)

Ta có: \(a = 2 > 0\) nên parabol quay bề lõm lên trên.

Đỉnh \(I\left( { - \frac{1}{2};\frac{1}{2}} \right).\) Trục đối xứng \(x =  - \frac{1}{2}.\) giao điểm của hàm số với trục \(Oy\) là: \(\left( {0;1} \right).\) Đồ thị hàm số không có giao điểm với trục \(Ox.\) Lấy điểm \(\left( {1;5} \right)\) thuộc đồ thị hàm số, điểm đối xứng với điểm đó qua trục đối xứng \(x =  - \frac{1}{2}\) là: \(\left( { - 2;5} \right).\)

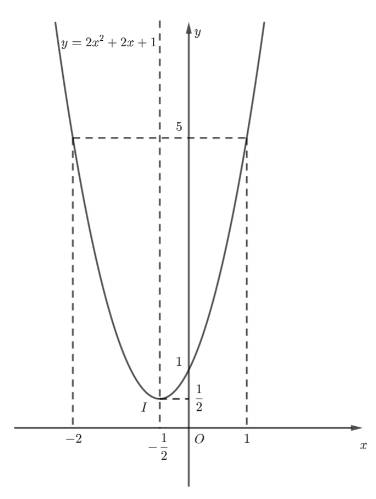
Tập giá trị của hàm số là: \(\left[ {\frac{1}{2}; + \infty } \right).\)

Từ đồ thị ta thấy: Hàm số \(y = 2{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \frac{1}{2}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{1}{2}} \right).\)

B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)

Nhìn vào đồ thị, ta thấy:

a) Hàm số \(y =  - 2x + 1\)nghịch biến trên \(\mathbb{R}\)

b) Hàm số \(y =  - \frac{1}{2}{x^2}\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)

a) Hệ số \(a = 5 > 0,b = 4 \Rightarrow \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.5}} = \frac{{ - 2}}{5}\)

Vậy hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{{ - 2}}{5}} \right)\) và đồng biến trên \(\left( {\frac{{ - 2}}{5}; + \infty } \right)\)

b) Ta có \(a =  - 2 < 0,b = 8\)

\( \Rightarrow  - \frac{b}{{2a}} = \frac{{ - 8}}{{2.\left( { - 2} \right)}} = 2\)

Vậy hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;2} \right)\) và nghịch biến trên khoảng \(\left( {2; + \infty } \right)\)

Câu 50: D

Còn câu 48,49 thì sao ạ.

Trục đối xứng của hàm số là: \(x = \frac{5}{2}.\)

Vì \(a = 1 > 0\) nên hàm số đồng biến trên khoảng \(\left( {\frac{5}{2}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;\frac{5}{2}} \right).\)

Chọn C.

Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)

Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)

Hàm số ở câu d) \(y = 5{x^2} + \sqrt x  + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)

Hàm số \(y =  - 3{x^2} + 1\) là hàm số bậc hai.