Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
\(2^{49}=\left(2^7\right)^7=128^7;5^{21}=\left(5^3\right)^7=125^7\\ Vì:128^7>125^7\Rightarrow2^{49}>5^{21}\)
Bài 2:
\(a,S=1+3+3^2+3^3+...+3^{99}\\ =\left(1+3+3^2+3^3\right)+3^4.\left(1+3+3^2+3^3\right)+...+3^{96}.\left(1+3+3^2+3^3\right)\\ =40+3^4.40+...+3^{96}.40\\ =40.\left(1+3^4+...+3^{96}\right)⋮40\\ b,S=1+4+4^2+4^3+...+4^{62}\\ =\left(1+4+4^2\right)+4^3.\left(1+4+4^2\right)+...+4^{60}.\left(1+4+4^2\right)\\ =21+4^3.21+...+4^{60}.21\\ =21.\left(1+4^3+...+4^{60}\right)⋮21\)
Bài 1 :
\(2^{49}=\left(2^7\right)^7=128^7\)
\(5^{21}=\left(5^3\right)^7=125^7\)
mà \(125^7< 128^7\)
\(\Rightarrow2^{49}>5^{21}\)
Bài 2 :
a) \(S=1+3+3^2+3^3+...3^{99}\)
\(\Rightarrow S=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)...+3^{96}\left(1+3+3^2+3^3\right)\)
\(\Rightarrow S=40+40.3^4+...+40.3^{96}\)
\(\Rightarrow S=40\left(1+3^4+...+3^{96}\right)⋮40\)
\(\Rightarrow dpcm\)
b) \(S=1+4+4^2+4^3+...4^{62}\)
\(\Rightarrow S=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...4^{60}\left(1+4+4^2\right)\)
\(\Rightarrow S=21+4^3.21+...4^{60}.21\)
\(\Rightarrow S=21\left(1+4^3+...4^{60}\right)⋮21\)
\(\Rightarrow dpcm\)

D = 1 + 4 + 4 2 + 4 3 + . . . + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 + 4 4 + 4 5 + ... + 4 57 + 4 58 + 4 59
= 1 + 4 + 4 2 + 4 3 . 1 + 4 + 4 2 + ... + 4 57 . 1 + 4 + 4 2
= 21 + 21 . 4 3 + . . . + 21 . 4 57 ⋮ 21

A=1+4+42+...+459A=1+4+42+...+459
A=(1+4)+(42+43)+...+(458+459)A=(1+4)+(42+43)+...+(458+459)
A=(1+4)+42(1+4)+...+458(1+4)A=(1+4)+42(1+4)+...+458(1+4)
A=5+42.5+...+448.5A=5+42.5+...+448.5
A=5(1+42+...+448)A=5(1+42+...+448)
⇒A⋮5
A=1+4+42+...+459A=1+4+42+...+459
A=(1+4+42)+(43+44+45)+...+(457+458+459)A=(1+4+42)+(43+44+45)+...+(457+458+459)
A=(1+4+42)+43(1+4+42)+...+447(1+4+42)A=(1+4+42)+43(1+4+42)+...+447(1+4+42)
A=21+43.21+...+447.21A=21+43.21+...+447.21
A=21(1+43+...+447)A=21(1+43+...+447)
⇒A⋮21
k cho mik đi mik cảm ơn

CM: A ⋮ 5
A = 1 + 4 + 42 + 43 + ... + 460
A = (1 + 4) + (42 + 43) + ... + (459 + 460)
A = 5 + 42 . (1 + 4) + ... + 459 . (1 + 4)
A = 5 + 42 . 5 + ... + 459 . 5
A = 5 . (1 + 42 + ... + 459) ⋮ 5
Vậy A ⋮ 5
CM: A ⋮ 21
A = 1 + 4 + 42 + 43 + ... + 460
A = (1 + 4 + 42) + (43 + 44 + 45) + ... + (458 + 459 + 460)
A = 21 + 43 . (1 + 4 + 42) + ... + 458 . (1 + 4 + 42)
A = 21 + 43 . 21 + ... + 458 . 21
A = 21 . (1 + 43 + ... + 458) ⋮ 21
Vậy A ⋮ 21

A= (21+22+23)+(24+25+26)+...+(258+259+260)
=20(21+22+23)+23(21+22+23)+...+257(21+22+23)
=(21+22+23)(20+23+...+257)
= 14(20+23+...+257) chia hết cho 7
Vậy A chia hết cho 7
gọi 1/41+1/42+1/43+...+1/80=S
ta có :
S>1/60+1/60+1/60+...+1/60
S>1/60 x 40
S>8/12>7/12
Vậy S>7/12

a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5

ta có
\(1+3+3^2+..+3^{2000}=\left(1+3+3^2\right)+\left(3^3+3^4+3^5\right)+..+\left(3^{1998}+3^{1999}+3^{2000}\right)\)
\(=13.1+13\cdot3^3+..+13\cdot3^{1998}\) chia hết cho 13
tương tự
\(1+4+4^2+..+4^{2012}=\left(1+4+4^2\right)+..+\left(4^{2010}+4^{2011}+4^{2012}\right)\)
\(=21.1+21\cdot4^3+..+21.4^{2010}\) chia hết cho 21
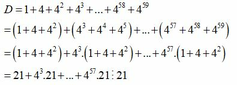

4A=4+4^2+4^3+.....+4^60
4A-A=(4+4^2+...+4^60)-(1+4+4^2+...+4^59)
3A=4^60-1
A=\(\frac{4^{60}-1}{3}\)
e hình như bạn giải lạc đề rồi