
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


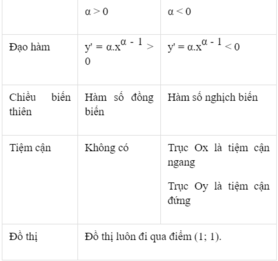
Bảng tóm tắt các tính chất của hàm số lũy thừa y = x α trên khoảng (0; + ∞)

Tính chất của lũy thừa với số mũ thực:
Cho a, b là những số thực dương; α,β là những số thực tùy ý. Khi đó ta có:
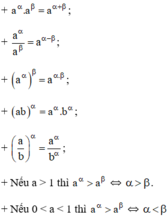

Đáp án C
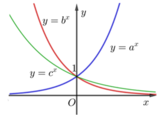
Dựa vào hình vẽ, ta thấy rằng:
Hàm số y = ax là hàm số đồng biến; hàm số y = bx, y = cx là hàm số nghịch biến.
Suy ra a > 1 và 0 < b < 1 0 < c < 1 → a > b ; c
Gọi B(-1; yB) thuộc đồ thị hàm số y = b x ⇒ y B = 1 b
Và C(-1;yc) thuộc đồ thị hàm số y = c x ⇒ y C = 1 c
Dựa vào đồ thị, ta có y B > y c ⇒ 1 b > 1 c ⇒ c > b

Hàm số mũ: y = a x
- Tập xác định: D = R.
- Chiều biến thiên:
+ y = a x .lna
a > 1 ⇒ y’ > 0 ⇒ Hàm số đồng biến trên R.
0 < a < 1 ⇒ y’ < 0 ⇒ Hàm số nghịch biến trên R.
+ Tiệm cận: 
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
- Đồ thị:
+ Đồ thị đi qua (0; 1) và (1; a).
+ Đồ thị nằm phía trên trục hoành.

- Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
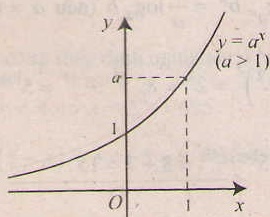
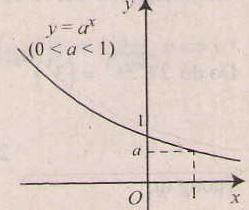
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
- Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = .
- Chiều biến thiên: Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
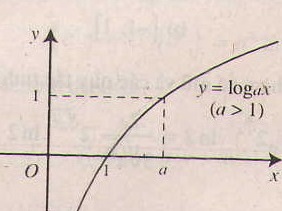
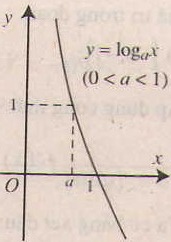


Bảng tóm tắt các tính chất của hàm số lũy thừa trên khoảng (0, +∞)
α > 0
α <0
Đạo hàm
Chiều biến thiên
Hàm số luôn đồng biến
Hàm số luôn nghịch biến
Tiệm cận
Không có
Tiệm cận ngang là Ox
Tiệm cận đứng là Oy
Đồ thị
Đồ thị luôn đi qua điểm (1, 1)