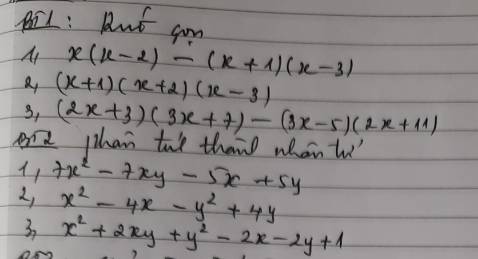Nếu \(x-2\ge0\Rightarrow x\ge2\Rightarrow\left|x-2\right|=x-2\)

Ta có phương trình 

\(x^2-6\left(x-2\right)-4=0\)

\(\Rightarrow x^2-6x+12-4=0\)

\(\Rightarrow x^2-6x+8=0\)

\(\Rightarrow x^2-2x-4x+8=0\)

\(\Rightarrow x\left(x-2\right)-4\left(x-2\right)=0\)

\(\Rightarrow\left(x-2\right)\left(x-4\right)=0\)

\(\Rightarrow x-2=0\) hoặc \(x-4=0\)

\(\left(+\right)x-2=0\Rightarrow x=2\) (tm)

\(\left(+\right)x-4=0\Rightarrow x=4\) (tm)

Nếu \(x-2<0\Rightarrow x<2\Rightarrow\left|x-2\right|=-\left(x-2\right)=2-x\)

Ta có phương trình 

\(x^2-6\left(2-x\right)-4=0\)

\(\Rightarrow x^2-12+6x-4=0\)

\(\Rightarrow x^2+6x-16=0\)

\(\Rightarrow x^2-2x+8x-16=0\)

\(\Rightarrow x\left(x-2\right)+8\left(x-2\right)=0\)

\(\Rightarrow\left(x-2\right)\left(x+8\right)=0\)

\(\Rightarrow x-2=0\) hoặc \(x+8=0\)

\(\left(+\right)x-2=0\Rightarrow x=2\) (không tm)

\(\left(+\right)x+8=0\Rightarrow x=-8\left(tm\right)\) 

Vậy phương trình có tập nghiệm \(S=\left\{-8;2;4\right\}\)

( x + 2 ) ( x + 3 ) ( x + 4 ) ( x + 5 ) - 24

= ( x² + 7x + 10 ) ( x² + 7x + 12 ) - 24

Đặt x² + 7x + 10 = y

Ta có : 

y² + 2y - 24 = ( y - 4 ) ( y + 6 ) = ( x² + 7x + 6 ) ( x² + 7x + 16 )

                    = ( x + 1 ) ( x + 6 ) ( x² + 7x + 16 )

Đặt x²+7x+10=t

\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24=\left[\left(x+2\right)\left(x+5\right)\right]\left[\left(x+3\right)\left(x+4\right)\right]\)

\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24=t\left(t+2\right)-24=t^2+2t-24\)

\(=\left(t^2+2t+1\right)-25=\left(t+1\right)^2-5^2=\left(t-4\right)\left(t+6\right)\)=(x²+7x+6)(x²+7x+16)

=(x²+x+6x+6)(x²+7x+16)=[x(x+1)+6(x+1)](x²+7x+16)=(x+1)(x+6)(x²+7x+16)

Gọi vận tốc ô tô 1 là x (km/h) (x>0)

thời gian ôtô 1 đi từ A đến điểm 2 xe gặp nhau: 10h30 - 6h = 4,5(h)

vận tốc ô tô 2 là x+20 (km/h)

thời gian oto 2 đi từ A đến điểm gặp nhau: 10h30-7h30 = 3h

Theo bài ra ta có phương trình:

4,5x = (x+20)3

=> 4,5x = 3x + 60

=> 1,5x = 60

=> x= 40 (tmdk)

hay vận tốc oto 1 là 40 km/h

vận tốc oto 2 là 40+20=60km/h

2:

1: =7x(x-y)-5(x-y)

=(x-y)(7x-5)

2: =(x^2-y^2)-(4x-4y)

=(x-y)(x+y)-4(x-y)

=(x-y)(x+y-4)

3: =(x^2+2xy+y^2)-(2x+2y)+1

=(x+y)^2-2(x+y)+1

=(x+y-1)^2

\(3a^2-6ab+3b^2-12c^2=3\left(a^2-2ab+b^2-4c^2\right)=3\left[\left(a-b\right)^2-\left(2c\right)^2\right]=3\left(a-b-2c\right)\left(a-b+2c\right)\)

Bài 1. (a) Điều kiện: \(x\ne\pm1\).

Ta có: \(A=\left(\dfrac{x-2}{x-1}-\dfrac{x+3}{x+1}+\dfrac{3}{x-1}\right):\left(1-\dfrac{x+3}{x+1}\right)\)

\(=\left(\dfrac{x-2+3}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-\left(x+3\right)}{x+1}\)

\(=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right):\dfrac{x+1-x-3}{x+1}\)

\(=\dfrac{\left(x+1\right)^2-\left(x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{-2}{x+1}\)

\(=\dfrac{x^2+2x+1-x^2-2x+3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}\)

\(=\dfrac{4}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{-2}=\dfrac{2}{1-x}\)

Vậy: \(A=\dfrac{2}{1-x}\)

(b) \(A=3\Leftrightarrow\dfrac{2}{1-x}=3\)

\(\Rightarrow1-x=\dfrac{2}{3}\Leftrightarrow x=\dfrac{1}{3}\left(TM\right)\)

Vậy: \(x=\dfrac{1}{3}\)

Bài 2. (a) Phương trình tương đương với:

\(\dfrac{3\left(3x-2\right)}{12}+\dfrac{6\left(x+3\right)}{12}=\dfrac{4\left(x-1\right)}{12}+\dfrac{x+1}{12}\)

\(\Rightarrow3\left(3x-2\right)+6\left(x+3\right)=4\left(x-1\right)+x+1\)

\(\Leftrightarrow9x-6+6x+18=4x-4+x+1\)

\(\Leftrightarrow10x=-15\Leftrightarrow x=-\dfrac{3}{2}\)

Vậy: Phương trình có tập nghiệm \(S=\left\{-\dfrac{3}{2}\right\}\).

(b) Điều kiện: \(x\ne\pm1\). Phương trình tương đương với:

\(\dfrac{2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}+\dfrac{2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x+1\right)\left(x-1\right)}\)

\(\Rightarrow2\left(x+1\right)+2\left(x-1\right)=2x^2+2\)

\(\Leftrightarrow2x+2+2x-2=2x^2+2\)

\(\Leftrightarrow2x^2-4x+2=0\Leftrightarrow2\left(x^2-2x+1\right)=0\)

\(\Leftrightarrow2\left(x-1\right)^2=0\Rightarrow x-1=0\Leftrightarrow x=1\left(KTM\right)\)

Vậy: Phương trình có tập nghiệm \(S=\varnothing\)