Bài 2: 

a: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có 

BH chung

HA=HD

Do đó: ΔBHA=ΔBHD

b: Ta có: ΔBHA=ΔBHD

nên \(\widehat{ABH}=\widehat{DBH}\)

hay BH là tia phân giác của góc ABD

6)  \(\dfrac{8^6}{256}=\dfrac{\left(2^3\right)^6}{2^8}=\dfrac{2^{18}}{2^8}=2^{10}=1024\)

7) \(\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{4}\right)^{20}=\left(\dfrac{1}{2}\right)^{15}.\left[\left(\dfrac{1}{2}\right)^2\right]^{20}=\left(\dfrac{1}{2}\right)^{15}.\left(\dfrac{1}{2}\right)^{40}=\left(\dfrac{1}{2}\right)^{55}=\dfrac{1}{2^{55}}\)

8)  \(\left(\dfrac{1}{9}\right)^{25}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{50}\div\left(\dfrac{1}{3}\right)^{30}=\left(\dfrac{1}{3}\right)^{20}=\dfrac{1}{3^{20}}\)

9)\(\left(\dfrac{1}{16}\right)^3\div\left(\dfrac{1}{8}\right)^2=\left(\dfrac{1}{2}\right)^{12}\div\left(\dfrac{1}{2}\right)^6=\left(\dfrac{1}{2}\right)^6=\dfrac{1}{64}\)

10)  \(\dfrac{27^2.8^5}{6^2.32^3}=\dfrac{3^6.2^{15}}{3^2.2^2.2^{15}}=\dfrac{3^4}{2^2}=\dfrac{81}{4}\)

Lần sau chụp hình rõ hơn nhé em. Hình mờ khó nhìn hình chính xác lắm

Bài 3:

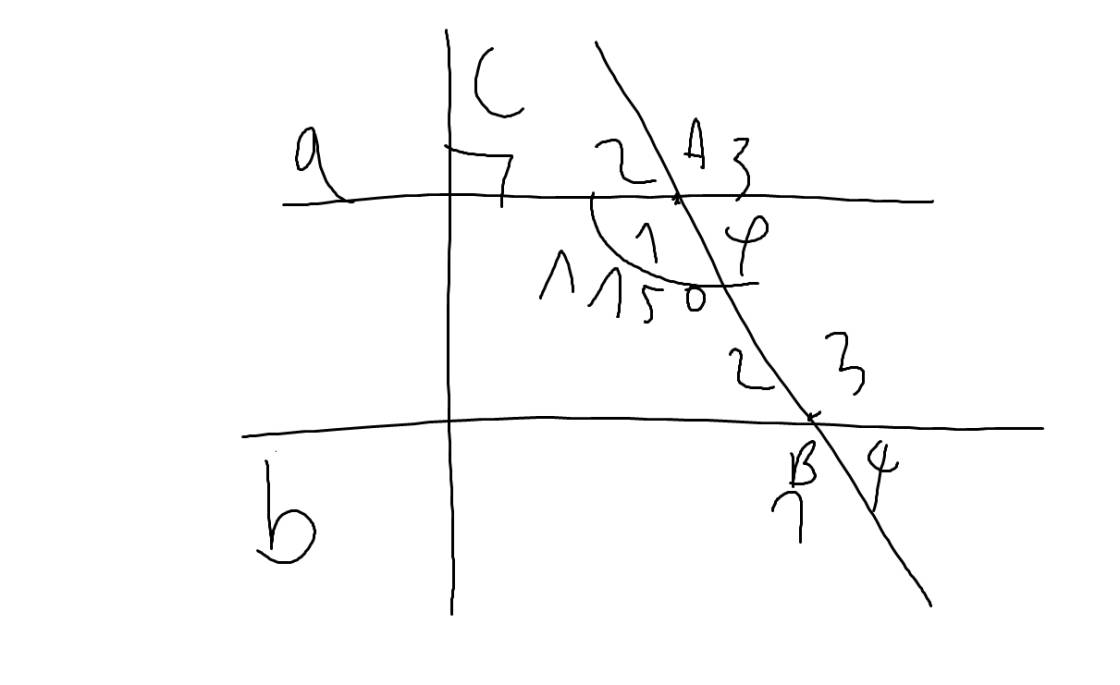
a) Do c ⊥ a

a // b

⇒ c ⊥ b

b) Ta có:

∠A₃ = ∠A₁ = 115⁰ (đối đỉnh)

Do a // b

⇒ ∠B₃ = ∠A₁ = 115⁰ (so le trong)

⇒ ∠B₁ = ∠B₃ = 115⁰ (đối đỉnh)

4:

a: Ot là phân giác của \(\widehat{AOB}\)

=>\(\widehat{tOB}=\widehat{tOA}=\dfrac{\widehat{AOB}}{2}=\dfrac{120^0}{2}=60^0\)

\(\widehat{tOB}=\widehat{yBO}\left(=60^0\right)\)

mà hai góc này là hai góc ở vị trí so le trong

nên Ot//By

b: \(\widehat{tOA}+\widehat{xAO}=180^0\)

mà hai góc này là hai góc ở vị trí trong cùng phía

nên Ot//Ax

Ax//Ot

Ot//By

Do đó: Ax//By

3:

a: a//b

c\(\perp\)a

Do đó: c\(\perp\)b

b: a//b

=>\(\widehat{A_1}+\widehat{B_2}=180^0\)(hai góc trong cùng phía)

=>\(\widehat{B_2}+115^0=180^0\)

=>\(\widehat{B_2}=65^0\)

a//b

=>\(\widehat{A_1}=\widehat{B_3}\)(hai góc so le trong)

mà \(\widehat{A_1}=115^0\)

nên \(\widehat{B_3}=115^0\)

\(\widehat{A_1}=\widehat{A_3}\)(hai góc đối đỉnh)

mà \(\widehat{A_1}=115^0\)

nên \(\widehat{A_3}=115^0\)

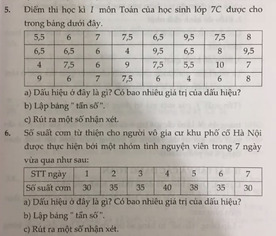
5.
a) Dấu hiệu: điểm thi HKI môn Toán của học sinh lớp 7C
Có 10 giá trị của dấu hiệu
b)

c)Số điểm thấp nhất: 4
Số điểm cao nhất: 10
Số điểm có nhiều nhất: 6
(bài 6 tương tự ạ)

Cảm ơn bạn

\(\left|2021x+2022\right|+\left|2021x-2021\right|=\left|2021x+2022\right|+\left|2021-2021x\right|\ge\left|2021x+2022+2021-2021x\right|=\left|4043\right|=4043\)

Dấu "=" xảy ra \(\Leftrightarrow\left(2021x+2022\right)\left(2021-2021x\right)\ge0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-\dfrac{2022}{2021}\\x\le1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-\dfrac{2022}{2021}\\x\ge1\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow-\dfrac{2022}{2021}\le x\le1\)

cảm ơn bạn nhiều ạ

Các số được điền vào các ô theo thứ tự từ trái sang phải là:

-1; - \(\dfrac{1}{3}\);  \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)

Bài 4: 

Diện tích xung quanh của hình hộp chữ nhật là:

\(\left(EH+CD\right)\cdot2\cdot EA=\left(8+6\right)\cdot2\cdot7=196\left(cm^2\right)\)

Thể tích của hình hộp chữ nhật là:

\(EA\cdot EH\cdot CD=7\cdot8\cdot6=336\left(cm^3\right)\)

giúp mình làm câu 3 tìm x đc k ạ cảm ơn ạ #xalxic