Tỉ lệ \(x=\dfrac{y}{-5}\)

x             -4                 -1                2                   3

y             20                 5               -10               -15

1)
a. Xét tg ABC cân tại A có AC=AB; gACB = g ABC.
Xét tg ACN và tg ABM có:
CN=BM (gt)
AC=AB
gACB=gABC
=> tg ACN = tg ABM (cgc)
=> AN=AM (2 cạnh tg ứng)
H là trung điểm BC nên AH là đường trung tuyến của tg ABC 
Mak tg ABC cân => H cũng là đường cao của tg ABC => AH ⊥ BC
b. Vì H là trung đ của BC nên CH=HB=BC/2= 3cm
Áp dụng định lý Py ta go vào tg AHB có:
AB^2=AH^2+HB^2
AH^2= AB^2 - HB^2
AH^2= 5^2 - 3^2 = 16 cm
=> AH= 4 cm
c. Xét tg AMN và tg KMB có:
AM=KM (gt)
MN=BM (gt)
gHMA=gKMB (đối đỉnh)
=> tg AMN = tg KMB (cgc)
d. tg AMN = tg KMB => gMAN=gMKB
=> AN=KB=Am
Mà AB>AM (quan hệ giữ đường xiêng và hình chiếu) nên AB>BK
=> gBKA> gBAK
=> gMAN>gBAM

Bổ sung câu 1b:
MN= BC/3=6/3=2 cm
MH= HN= MN/2= 1 cm
Áp dụng đl Py-ta-go vào tg AMH có
AM^2=AH^2+MH^2= 4^2+1^2= 17
=> AM= căn 17 cm

Bài 1: 

a) Áp dụng tích chất dãy tỉ số bằng nhau:

    \(\dfrac{x}{2}=\dfrac{y}{3}\)=\(\dfrac{x+y}{2+3}\)=\(\dfrac{-15}{5}\)= -3

=> x= -3.2= -6; y= -3.3= -9.

b) Áp dụng tích chất dãy tỉ số bằng nhau:

    \(\dfrac{x}{3}=\dfrac{y}{4}\)=\(\dfrac{x-y}{3-4}\)=\(\dfrac{12}{-1}\)= -12

=> x= -12.3= -36; y= -12.4= -48

c) 3x=7y=\(\dfrac{x}{7}=\dfrac{y}{3}\)

    Áp dụng tích chất dãy tỉ số bằng nhau:

    \(\dfrac{x}{y}=\dfrac{y}{3}=\dfrac{x-y}{7-3}=\dfrac{-16}{4}=-4\)

=> x= -4.7= -28; y= -4.3= -12

d) \(\dfrac{x}{y}=\dfrac{17}{13}=\dfrac{x}{17}=\dfrac{y}{13}\)

    Áp dụng tích chất dãy tỉ số bằng nhau:

     \(\dfrac{x}{17}=\dfrac{y}{13}=\dfrac{x+y}{17+13}=\dfrac{-60}{30}=-2\)

=> x= -2.17= -34; y= -2.13= -26

e) Áp dụng tính chất dãy tỉ số bằng nhau:

    \(\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)

=>x= 9= \(3^2\)= 3.4= 12; y= 16= \(4^2\)= 4.4= 16

Bài 2: 

2x=3y=\(\dfrac{x}{3}=\dfrac{y}{2}\); 5y=7z=\(\dfrac{y}{7}=\dfrac{z}{5}\)

-> \(\dfrac{x}{3}=\dfrac{y}{2};\dfrac{y}{7}=\dfrac{z}{5}\) = \(\dfrac{x}{21}=\dfrac{y}{14};\dfrac{y}{14}=\dfrac{z}{10}\)=> \(\dfrac{x}{21}=\dfrac{y}{14}=\dfrac{z}{10}\) =     \(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)

   Áp dụng tích chất dãy tỉ số bằng nhau:

\(\dfrac{3x}{63}=\dfrac{7y}{98}=\dfrac{5z}{50}\)=\(\dfrac{3x-7y+5z}{63-98+50}\)=\(\dfrac{30}{15}=2\)

=> x= 2.21= 42

=> y= 2.14= 28

=> z= 2.10= 20

Bài 2: 

Áp dụng tính chất của dãy tỉ số bằng nhau,ta được

\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{45}{9}=5\)

Do đó: a=10; b=15;c=20

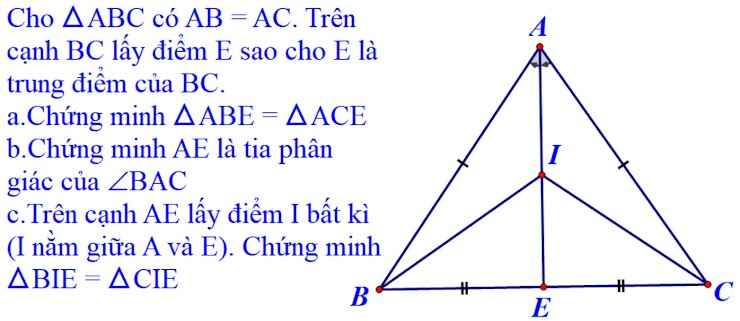
a) Xét tam giác ABE và tam giác ACE có:

+ AE chung.

+ AB = AC (gt).

+ BE = CE (E là trung điểm của BC).

=> Tam giác ABE = Tam giác ACE (c - c - c).

b) Xét tam giác ABC có: AB = AC (gt).

=> Tam giác ABC cân tại A.

Mà AE là đường trung tuyến (E là trung điểm của BC).

=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).

c) Xét tam giác ABC cân tại A có: 

AE là phân giác ^BAC (cmt).

=> AE là đường cao (Tính chất các đường trong tam giác cân).

=> AE \(\perp\) BC.

Xét tam giác BIE và tam giác CIE:

+ IE chung.

+ BE = CE (E là trung điểm của BC).

+ ^BEI = ^CEI ( = 90^o).

=> Tam giác BIE = Tam giác CIE (c - g - c).

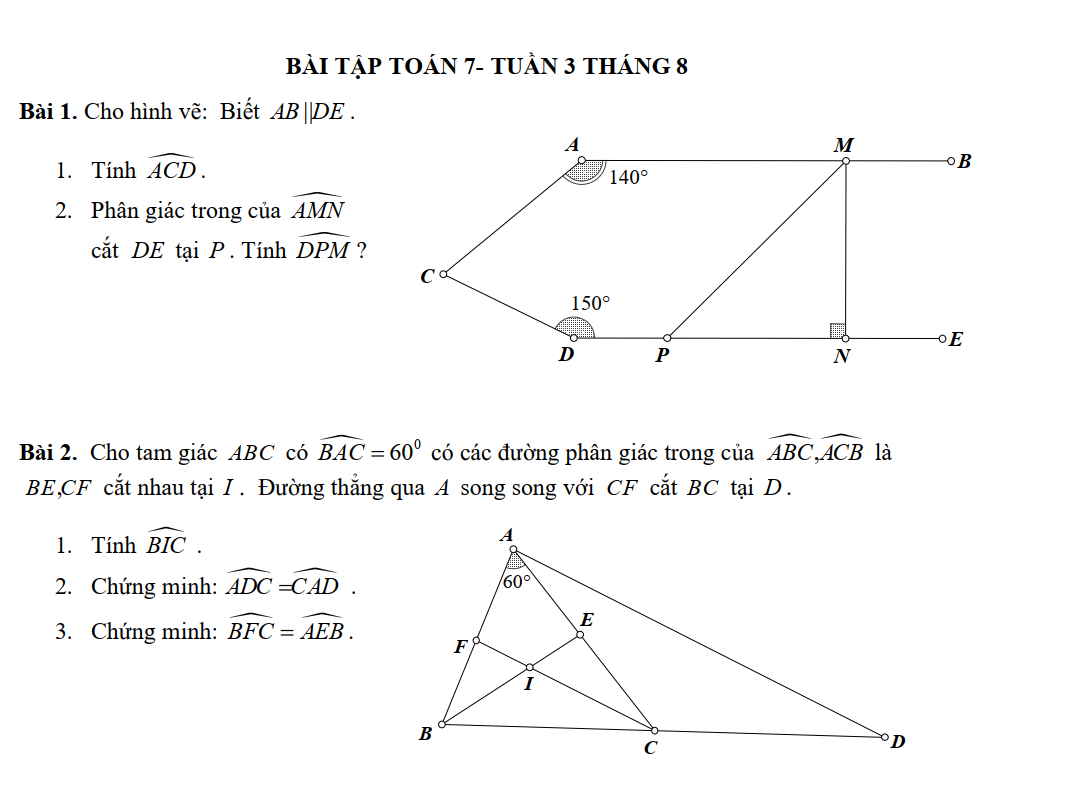
Bài 1: 

1) Kẻ tia Cx//AB//DE

Ta có: Cx//AB

\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)

\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)

Ta có: Cx//DE

\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)

\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)

\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)

2) Ta có AB//DE(gt)

         Mà DE⊥MN

=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))

Ta có AB//DE

=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)

\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)

bạn ơi giúp mình nốt bài 2 đi mình không biết làm